

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Baguenaudier
المؤلف:
Culin, S.
المصدر:
"Ryou-Kaik-Tjyo--Delay Guest Instrument (Ring Puzzle)." §20 in Games of the Orient: Korea, China, Japan. Rutland, VT: Charles E. Tuttle
الجزء والصفحة:
...
16-10-2021
2758
Baguenaudier
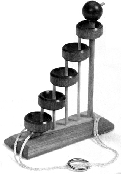
A puzzle involving disentangling a set of rings from a looped double rod, originally used by French peasants to lock chests (Steinhaus 1999). The word "baguenaudier" means "time-waster" in French, and the puzzle is also called the Chinese rings or Devil's needle puzzle. ("Bague" also means "ring," but this appears to be an etymological coincidence. Interestingly, the bladder-senna tree is also known as "baguenaudier" in French.) Culin (1965) attributes the puzzle to Chinese general Hung Ming (A.D. 181-234), who gave it to his wife as a present to occupy her while he was away at the wars.
The solution of the baguenaudier is intimately related to the theory of Gray codes.
The minimum number of moves 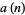 needed for
needed for 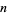 rings is
rings is
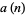 |
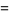 |
![[2/3(2^n-1)]](https://mathworld.wolfram.com/images/equations/Baguenaudier/Inline5.gif) |
(1) |
 |
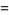 |
(2) |
where ![[x]](https://mathworld.wolfram.com/images/equations/Baguenaudier/Inline9.gif) is the ceiling function, giving 1, 2, 5, 10, 21, 42, 85, 170, 341, 682, ... (OEIS A000975). The generating function for these numbers is
is the ceiling function, giving 1, 2, 5, 10, 21, 42, 85, 170, 341, 682, ... (OEIS A000975). The generating function for these numbers is
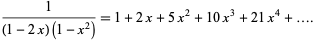 |
(3) |
They are also given by the recurrence relation
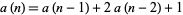 |
(4) |
with 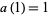 and
and 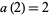 .
.
By simultaneously moving the two end rings, the number of moves for 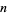 rings can be reduced to
rings can be reduced to
|
(5) |
giving 1, 1, 4, 7, 16, 31, 64, 127, 256, 511, ... (OEIS A051049).
Defining the complexity of a solution as the minimal number of times the ring passes through the arc from the last ring to the base of the puzzle, the minimal complexity of a solution is 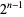 , as conjectured by Kauffman (1996) and proved by Przytycki and Sikora (2000).
, as conjectured by Kauffman (1996) and proved by Przytycki and Sikora (2000).
REFERENCES:
Culin, S. "Ryou-Kaik-Tjyo--Delay Guest Instrument (Ring Puzzle)." §20 in Games of the Orient: Korea, China, Japan. Rutland, VT: Charles E. Tuttle, pp. 31-32, 1965.
Dubrovsky, V. "Nesting Puzzles, Part II: Chinese Rings Produce a Chinese Monster." Quantum 6, 61-65 (Mar.) and 58-59 (Apr.), 1996.
Elliott Avedon Museum and Archive of Games, University of Waterloo, Ontario, Canada. "Wire and Ring Puzzles." http://www.ahs.uwaterloo.ca/~museum/puzzles/wire/.
Gardner, M. "The Binary Gray Code." In Knotted Doughnuts and Other Mathematical Entertainments. New York: W. H. Freeman, pp. 15-17, 1986.
Kauffman, L. H. "Tangle Complexity and the Topology of the Chinese Rings." In Mathematical Approaches to Biomolecular Structure and Dynamics. New York: Springer-Verlag, pp. 1-10, 1996.
Kraitchik, M. "Chinese Rings." §3.12.3 in Mathematical Recreations. New York: W. W. Norton, pp. 89-91, 1942.
Przytycki, J. H. and Sikora, A. S. "Topological Insights from the Chinese Rings." 21 Jul 2000. http://arxiv.org/abs/math.GT/0007134.
Sloane, N. J. A. Sequences A000975 and A051049 in "The On-Line Encyclopedia of Integer Sequences."
Slocum, J. and Botermans, J. Puzzles Old and New: How to Make and Solve Them. Seattle, WA: University of Washington Press, p. 105, 1988.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 268-269, 1999.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















