


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-8-2021
Date: 22-9-2016
Date: 11-7-2021
|
 |
 |
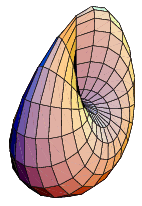
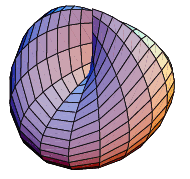
The self-intersection of a one-sided surface. The word "cross-cap" is sometimes also written without the hyphen as the single word "crosscap." The cross-cap can be thought of as the object produced by puncturing a surface a single time, attaching two zips around the puncture in the same direction, distorting the hole so that the zips line up, requiring that the surface intersect itself, and then zipping up. The cross-cap can also be described as a circular hole which, when entered, exits from its opposite point (from a topological viewpoint, both singular points on the cross-cap are equivalent).
The cross-cap has a segment of double points which terminates at two "pinch points." A cross-handle is homeomorphic to two cross-caps (Francis and Weeks 1999).
A sphere with one cross-cap has traditionally been called a real projective plane. While this is appropriate in the study of projective geometry when an affine structure is present, J. H. Conway advocates use of the term cross surface in a purely topological interpretation (Francis and Weeks 1999). The cross-cap is one of the three possible surfaces obtained by sewing a Möbius strip to the edge of a disk. The other two are the Boy surface and Roman surface.
A sphere with two cross-caps having coinciding boundaries is topologically equivalent to a Klein bottle (Francis and Weeks 1999). The surface with three cross-caps is known as Dyck's surface (Francis and Collins 1993, Francis and Weeks 1999).
The cross-cap can be generated using the general method for nonorientable surfaces using the polynomial function
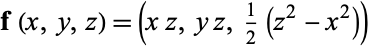 |
(1) |
(Pinkall 1986). Transforming to spherical coordinates gives
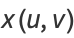 |
 |
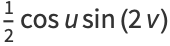 |
(2) |
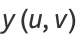 |
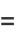 |
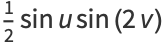 |
(3) |
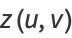 |
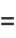 |
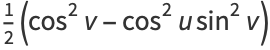 |
(4) |
for 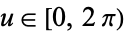 and
and ![v in [0,pi/2]](https://mathworld.wolfram.com/images/equations/Cross-Cap/Inline11.gif) . To make the equations slightly simpler, all three equations are normally multiplied by a factor of 2 to clear the arbitrary scaling constant. Three views of the cross-cap generated using this equation are shown above. Note that the middle one looks suspiciously like Bour's minimal surface.
. To make the equations slightly simpler, all three equations are normally multiplied by a factor of 2 to clear the arbitrary scaling constant. Three views of the cross-cap generated using this equation are shown above. Note that the middle one looks suspiciously like Bour's minimal surface.
Another representation is
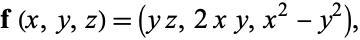 |
(5) |
(Gray 1997), giving parametric equations
 |
 |
 |
(6) |
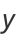 |
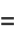 |
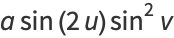 |
(7) |
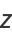 |
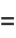 |
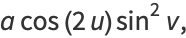 |
(8) |
(Geometry Center) where, for aesthetic reasons, the 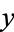 - and
- and 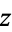 -coordinates have been multiplied by 2 to produce a squashed, but topologically equivalent, surface. It is therefore a quartic surface given by
-coordinates have been multiplied by 2 to produce a squashed, but topologically equivalent, surface. It is therefore a quartic surface given by
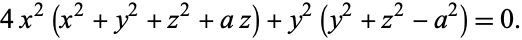 |
(9) |
The volume enclosed by the surface in this parametrization is
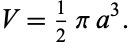 |
(10) |
The moment of inertia tensor for the solid with uniform density 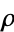 and mass
and mass 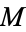 is given by
is given by
![I=[7/(16)Ma^2 0 ; 0 (59)/(240)Ma^2 0; 0 0 (11)/(40)Ma^2].](https://mathworld.wolfram.com/images/equations/Cross-Cap/NumberedEquation5.gif) |
(11) |
Taking the inversion of a cross-cap such that (0, 0, 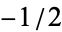 ) is sent to
) is sent to 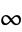 gives Plücker's conoid, shown above (Pinkall 1986).
gives Plücker's conoid, shown above (Pinkall 1986).
REFERENCES:
Fischer, G. (Ed.). Plate 107 in Mathematische Modelle aus den Sammlungen von Universitäten und Museen, Bildband. Braunschweig, Germany: Vieweg, p. 108, 1986.
Francis, G. and Collins, B. "On Knot-Spanning Surfaces: An Illustrated Essay on Topological Art." Ch. 11 in The Visual Mind: Art and Mathematics (Ed. M. Emmer). Cambridge, MA: MIT Press, 1993.
Francis, G. K. and Weeks, J. R. "Conway's ZIP Proof." Amer. Math. Monthly 106, 393-399, 1999.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 15, 1984.
Geometry Center. "The Crosscap." https://www.geom.umn.edu/zoo/toptype/pplane/cap/.
Gray, A. "The Cross Cap." Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 333-335, 1997.
Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, p. 64, 1986.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 197, 1991.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|