Braid Group

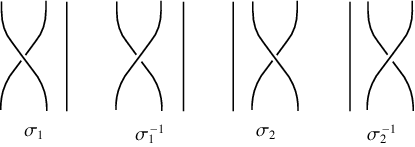
Consider 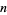 strings, each oriented vertically from a lower to an upper "bar." If this is the least number of strings needed to make a closed braid representation of a link,  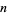is called the braid index. A general 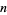-braid is constructed by iteratively applying the  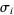(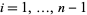) operator, which switches the lower endpoints of the 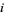th and 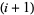th strings--keeping the upper endpoints fixed--with the 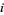th string brought above the 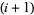th string. If the 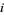th string passes below the 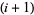th string, it is denoted .

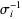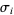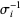The operations  and  on 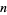 strings define a group known as the braid group or Artin braid group, denoted .

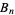Topological equivalence for different representations of a braid wor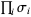d  and 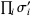 is guaranteed by the conditions

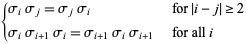(1)

as first proved by E. Artin.

Any 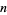-braid can be expressed as a braid word, e.g.,  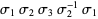is a braid word in the braid group 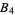. When the opposite ends of the braids are connected by nonintersecting lines, knots (or links) may formed that can be labeled by their corresponding braid word. The Burau representation gives a matrix representation of the braid groups.

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 132-133, 1994.

Birman, J. S. "Braids, Links, and the Mapping Class Groups." Ann. Math. Studies, No. 82. Princeton, NJ: Princeton University Press, 1976.

Birman, J. S. "Recent Developments in Braid and Link Theory." Math. Intell. 13, 52-60, 1991.

Christy, J. "Braids." http://library.wolfram.com/infocenter/MathSource/813/.

Jones, V. F. R. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.

Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.