


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-5-2021
Date: 2-3-2021
Date: 22-2-2021
|
There are at least two distinct notions of an intensity function related to the theory of point processes.
In some literature, the intensity 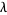 of a point process
of a point process 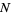 is defined to be the quantity
is defined to be the quantity
![lambda=lim_(hv0)(Pr{N(0,h]>0})/h](https://mathworld.wolfram.com/images/equations/IntensityFunction/NumberedEquation1.gif) |
(1) |
provided it exists. Here, 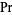 denotes probability. In particular, it makes sense to talk about point processes having infinite intensity, though when finite,
denotes probability. In particular, it makes sense to talk about point processes having infinite intensity, though when finite, 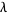 allows
allows 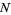 to be rewritten so that
to be rewritten so that
![Pr{N(x,x+h]>0}=lambdah+o(h)](https://mathworld.wolfram.com/images/equations/IntensityFunction/NumberedEquation2.gif) |
(2) |
as 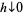 where here,
where here, 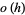 denotes little-O notation (Daley and Vere-Jones 2007).
denotes little-O notation (Daley and Vere-Jones 2007).
Other authors define the function 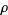 to be an intensity function of a point process
to be an intensity function of a point process 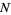 provided that
provided that 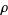 is a density of the intensity measure
is a density of the intensity measure 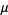 associated to
associated to 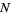 relative to Lebesgue measure, i.e.,if for all Borel sets
relative to Lebesgue measure, i.e.,if for all Borel sets 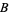 in
in 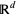 ,
,
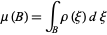 |
(3) |
where 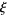 denotes Lebesgue measure (Pawlas 2008).
denotes Lebesgue measure (Pawlas 2008).
REFERENCES:
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.
Pawlas, Z. "Spatial Modeling and Spatial Statistics." Course Notes. Autumn 2008. https://www.math.ku.dk/~pawlas/rumlig.pdf.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|