


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-4-2021
Date: 19-2-2021
Date: 22-3-2021
|
The sample variance 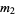 (commonly written
(commonly written 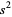 or sometimes
or sometimes 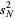 ) is the second sample central moment and is defined by
) is the second sample central moment and is defined by
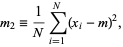 |
(1) |
where 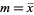 the sample mean and
the sample mean and 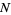 is the sample size.
is the sample size.
To estimate the population variance 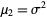 from a sample of
from a sample of 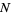 elements with a priori unknown mean (i.e., the mean is estimated from the sample itself), we need an unbiased estimator
elements with a priori unknown mean (i.e., the mean is estimated from the sample itself), we need an unbiased estimator 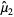 for
for 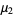 . This estimator is given by k-statistic
. This estimator is given by k-statistic 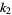 , which is defined by
, which is defined by
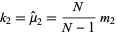 |
(2) |
(Kenney and Keeping 1951, p. 189). Similarly, if 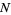 samples are taken from a distribution with underlying central moments
samples are taken from a distribution with underlying central moments 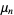 , then the expected value of the observed sample variance
, then the expected value of the observed sample variance 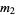 is
is
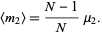 |
(3) |
Note that some authors (e.g., Zwillinger 1995, p. 603) prefer the definition
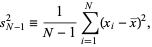 |
(4) |
since this makes the sample variance an unbiased estimator for the population variance. The distinction between 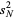 and
and 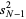 is a common source of confusion, and extreme care should be exercised when consulting the literature to determine which convention is in use, especially since the uninformative notation
is a common source of confusion, and extreme care should be exercised when consulting the literature to determine which convention is in use, especially since the uninformative notation 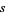 is commonly used for both. The unbiased sample variance
is commonly used for both. The unbiased sample variance 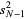 is implemented as Variance[list].
is implemented as Variance[list].
Also note that, in general, 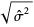 is not an unbiased estimator of the standard deviation
is not an unbiased estimator of the standard deviation 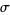 even if
even if 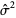 is an unbiased estimator for
is an unbiased estimator for 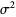 .
.
REFERENCES:
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 16, 2000.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, 1995.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|