المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Somer-Lucas Pseudoprime |
 846
 03:19 مساءً
date: 25-1-2021 |
Author : Ribenboim, P. 
Book or Source : "Somer-Lucas Pseudoprimes." §2.X.D in The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag 
Page and Part : pp. 131-132|
Read More
Date: 20-7-2020
2373
Date: 5-12-2020
784
Date: 31-10-2019
931
|
An odd composite number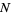 
is called a Somer-Lucas 
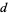-pseudoprime (with 
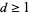) if there exists a nondegenerate Lucas sequence 
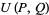with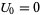 
, 
, 
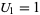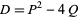, such that 
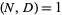and the rank appearance of 
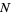in the sequence 
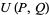is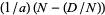 
, where 
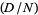denotes the Jacobi symbol.
REFERENCES:
Ribenboim, P. "Somer-Lucas Pseudoprimes." §2.X.D in The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 131-132, 1996.
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|
