


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-10-2019
Date: 23-11-2019
Date: 29-10-2019
|
A Carmichael number is an odd composite number 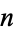 which satisfies Fermat's little theorem
which satisfies Fermat's little theorem
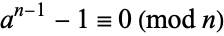 |
(1) |
for every choice of 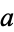 satisfying
satisfying 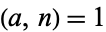 (i.e.,
(i.e., 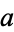 and
and 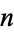 are relatively prime) with
are relatively prime) with 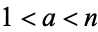 . A Carmichael number is therefore a pseudoprime to any base. Carmichael numbers therefore cannot be found to be composite using Fermat's little theorem. However, if
. A Carmichael number is therefore a pseudoprime to any base. Carmichael numbers therefore cannot be found to be composite using Fermat's little theorem. However, if 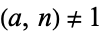 , the congruence of Fermat's little theorem is nonzero, thus identifying a Carmichael number
, the congruence of Fermat's little theorem is nonzero, thus identifying a Carmichael number 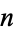 as composite.
as composite.
Carmichael numbers are sometimes called "absolute pseudoprimes" and also satisfy Korselt's criterion. R. D. Carmichael first noted the existence of such numbers in 1910, computed 15 examples, and conjectured that there were infinitely many. In 1956, Erdős sketched a technique for constructing large Carmichael numbers (Hoffman 1998, p. 183), and a proof was given by Alford et al. (1994).
Any solution to Lehmer's totient problem must be a Carmichael number.
The first few Carmichael numbers are 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, 29341, ... (OEIS A002997). The number of Carmichael numbers less than 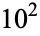 ,
, 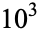 , ... are 0, 1, 7, 16, 43, 105, ... (OEIS A055553; Pinch 1993). The smallest Carmichael numbers having 3, 4, ... factors are
, ... are 0, 1, 7, 16, 43, 105, ... (OEIS A055553; Pinch 1993). The smallest Carmichael numbers having 3, 4, ... factors are 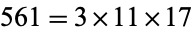 ,
, 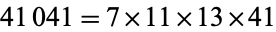 , 825265, 321197185, ... (OEIS A006931).
, 825265, 321197185, ... (OEIS A006931).
Carmichael numbers have at least three prime factors. For Carmichael numbers with exactly three prime factors, once one of the primes has been specified, there are only a finite number of Carmichael numbers which can be constructed. Indeed, for Carmichael numbers with 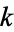 prime factors, there are only a finite number with the least
prime factors, there are only a finite number with the least 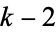 specified.
specified.
Numbers of the form 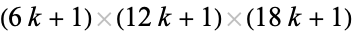 are Carmichael numbers if each of the factors is prime (Korselt 1899, Ore 1988, Guy 1994). This can be seen since for
are Carmichael numbers if each of the factors is prime (Korselt 1899, Ore 1988, Guy 1994). This can be seen since for
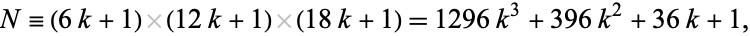 |
(2) |
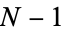 is a multiple of
is a multiple of 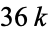 and the least common multiple of
and the least common multiple of 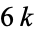 ,
, 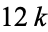 , and
, and 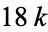 is
is 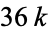 , so
, so 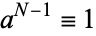 modulo each of the primes
modulo each of the primes 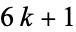 ,
, 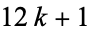 , and
, and 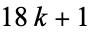 , hence
, hence 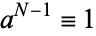 modulo their product. The first few such Carmichael numbers correspond to
modulo their product. The first few such Carmichael numbers correspond to 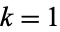 , 6, 35, 45, 51, 55, 56, ... (OEIS A046025) and are 1729, 294409, 56052361, 118901521, ... (OEIS A033502).
, 6, 35, 45, 51, 55, 56, ... (OEIS A046025) and are 1729, 294409, 56052361, 118901521, ... (OEIS A033502).
Let 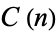 denote the number of Carmichael numbers less than
denote the number of Carmichael numbers less than 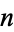 . Then, for all sufficiently large
. Then, for all sufficiently large 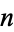 ,
,
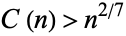 |
(3) |
(Alford et al. 1994), which proves that there are infinitely many Carmichael numbers. The upper bound
 |
(4) |
has also been proved (R. G. E. Pinch).
The Carmichael numbers have the following properties:
1. If a prime 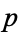 divides the Carmichael number
divides the Carmichael number 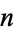 , then
, then 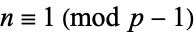 implies that
implies that 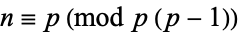 .
.
2. Every Carmichael number is squarefree.
3. An odd composite squarefree number 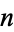 is a Carmichael number iff
is a Carmichael number iff 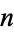 divides the denominator of the Bernoulli number
divides the denominator of the Bernoulli number 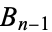 .
.
The largest known Carmichael numbers having a given number of factors are summarized in the following table (updated from Dubner 1989, 1998).
| factors | digits | discoverer |
| 3 | 60351 | Broadhurst (2002) |
| 4 | 29094 | Broadhurst 2003 (Broadhurst 2015b) |
| 5 | 1015 | Caldwell and Dubner |
| 6 | 19140 | Broadhurst 2003 (Broadhurst 2015a) |
REFERENCES:
Alford, W. R.; Granville, A.; and Pomerance, C. "There are Infinitely Many Carmichael Numbers." Ann. Math. 139, 703-722, 1994.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 87, 1987.
Broadhurst, D. "60351-digit 3-Carmichael number." 2 Dec 2002. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0212&L=nmbrthry&P=R2.
Broadhurst, D. "Re: 14241 digits 5-Carmichael number." 29 Aug 2015a. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind1508&L=NMBRTHRY&P=R628.
Broadhurst, D. "Re: 25791 digits 4-Carmichael number." 29 Aug 2015b. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind1508&L=NMBRTHRY&P=6285.
Carlini, A. and Hosoya, A. "Carmichael Numbers on a Quantum Computer." 5 Aug 1999. https://arxiv.org/abs/quant-ph/9908022.
Carmichael, R. D. "Note on a New Number Theory Function." Bull. Amer. Math. Soc. 16, 232-238, 1910.
Dubner, H. "A New Method for Producing Large Carmichael Numbers." Math. Comput. 53, 411-414, 1989.
Dubner, H. "Carmichael Number Record." 11 Sep 1998. https://listserv.nodak.edu/scripts/wa.exe?A2=ind9809&L=NMBRTHRY&P=795.
Guy, R. K. "Carmichael Numbers." §A13 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 30-32, 1994.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 182-183, 1998.
Korselt, A. "Problème chinois." L'intermédiaire math. 6, 143-143, 1899.
Ore, Ø. Number Theory and Its History. New York: Dover, 1988.
Pinch, R. G. E. "The Carmichael Numbers up to 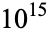 ." Math. Comput. 61, 381-391, 1993a.
." Math. Comput. 61, 381-391, 1993a.
Pinch, R. G. E. "Some Primality Testing Algorithms." Not. Amer. Math. Soc. 40, 1203-1210, 1993b.
Pinch, R. G. E. ftp://ftp.dpmms.cam.ac.uk/pub/Carmichael/table.
Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. "The Pseudoprimes to 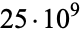 ." Math. Comput. 35, 1003-1026, 1980.
." Math. Comput. 35, 1003-1026, 1980.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 118-125, 1996.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Basel: Birkhäuser, pp. 89-90 and 94-95, 1994.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 116, 1993.
Sloane, N. J. A. Sequences A002997/M5462, A006931/M5463, A033502, A046025, and A055553 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|