
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-7-2020
Date: 5-8-2020
Date: 20-8-2020
|
A number which is simultaneously a heptagonal number 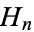 and pentagonal number
and pentagonal number 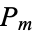 . Such numbers exist when
. Such numbers exist when
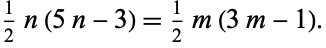 |
(1) |
Completing the square and rearranging gives
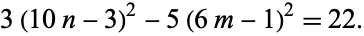 |
(2) |
Substituting 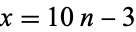 and
and 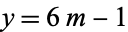 gives the Pell-like quadratic Diophantine equation
gives the Pell-like quadratic Diophantine equation
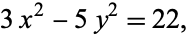 |
(3) |
which has solutions 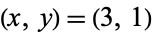 , (7, 5), (17, 13), (53, 41), (133, 103), .... The integer solutions in
, (7, 5), (17, 13), (53, 41), (133, 103), .... The integer solutions in 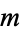 and
and 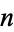 are then given by
are then given by 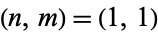 , (42, 54), (2585, 3337), (160210, 206830), (9930417, 12820113) ... (OEIS A046198 and A046199), corresponding to the heptagonal pentagonal numbers 1, 4347, 16701685, 64167869935, 246532939589097, ... (OEIS A048900).
, (42, 54), (2585, 3337), (160210, 206830), (9930417, 12820113) ... (OEIS A046198 and A046199), corresponding to the heptagonal pentagonal numbers 1, 4347, 16701685, 64167869935, 246532939589097, ... (OEIS A048900).
REFERENCES:
Sloane, N. J. A. Sequences A046198, A046199, and A048900 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|