Thâbit ibn Kurrah Rule

Thâbit ibn Kurrah's rules is a beautiful result of Thâbit ibn Kurrah dating back to the tenth century (Woepcke 1852; Escott 1946; Dickson 2005, pp. 5 and 39; Borho 1972). Take 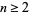 and suppose that

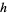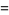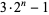			(1)
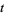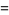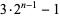			(2)
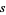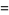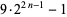			(3)

are all prime. Then 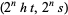 are an amicable pair, where  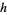is sometimes called a Thâbit ibn Kurrah number. This form was rediscovered by Fermat in 1636 and Descartes in 1638 and generalized by Euler to Euler's rule (Borho 1972).

In order for such numbers to exist, there must be prime 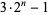 for two consecutive 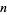, leaving only the possibilities 1, 2, 3, 4, and 6, 7. Of these,  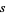is prime for 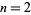, 4, and 7, giving the amicable pairs (220, 284), (17296, 18416), and (9363584, 9437056).

In fact, various rules can be found that are analogous to Thâbit ibn Kurrah's. Denote a "Thâbit rule" by 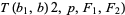 for given natural numbers  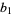and 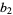, a prime  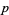not dividing 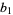, , 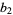and polynomials . Then a necessary condition for the set of amicable pairs 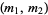 of the form  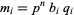(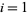, 2) with 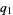,  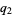prime and  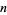a natural number to be infinite is that

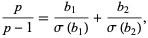(4)

where 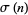 is the divisor function (Borho 1972). As a result,  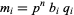(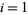, 2) form an amicable pair, if for some 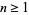, both

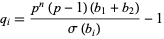(5)

for 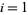, 2 are prime integers not dividing  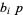(Borho 1972).

The following table summarizes some of the known Thâbit ibn Kurrah rules 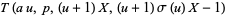 (Borho 1972, te Riele 1974).

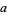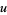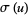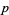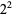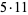		72	127
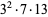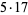		108	193
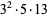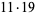		240	449
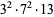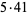		252	457
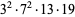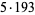		1164	2129
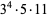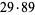		2700	5281
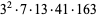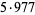		5868	10753
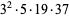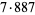		7104	13313
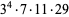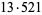		7308	14081
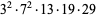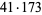		7308	14401
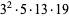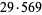		17100	33601
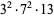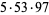		31752	57457
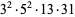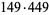		67500	134401
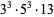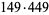		67500	134401
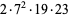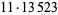		162288	311041
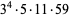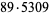		477900	950401
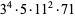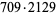		1512300	3021761
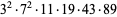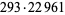		6750828	13478401
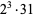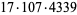		8436960	16329601
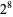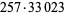		8520192	17007103
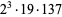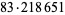		18366768	36514801
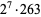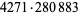		1199936448	2399587741

REFERENCES:

Borho, W. "On Thabit ibn Kurrah's Formula for Amicable Numbers." Math. Comput. 26, 571-578, 1972.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, 2005.

Escott, E. B. E. "Amicable Numbers." Scripta Math. 12, 61-72, 1946.

Riesel, H. "Lucasian Criteria for the Primality of 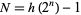." Math. Comput. 23, 869-875, 1969.

Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Basel: Birkhäuser, p. 394, 1994.

Sloane, N. J. A. Sequence A002235/M0545 in "The On-Line Encyclopedia of Integer Sequences."

te Riele, H. J. J. "Four Large Amicable Pairs." Math. Comput. 28, 309-312, 1974.

Woepcke, F. J. Asiatique 20, 320-429, 1852.