Real Number

The field of all rational and irrational numbers is called the real numbers, or simply the "reals," and denoted 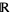. The set of real numbers is also called the continuum, denoted 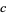. The set of reals is called Reals in the Wolfram Language, and a number  can be tested to see if it is a member of the reals using the command Element[x, Reals], and expressions that are real numbers have the Head of Real.

The real numbers can be extended with the addition of the imaginary number i, equal to 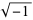. Numbers of the form 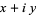, where  and 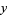 are both real, are called complex numbers, which also form a field. Another extension which includes both the real numbers and the infinite ordinal numbers of Georg Cantor is the surreal numbers.

"Plouffe's Inverter" includes a huge database of 54 million real numbers which are algebraically related to fundamental mathematical constants and functions.

Almost all real numbers are lexicons, meaning that they do not obey probability laws such as the law of large numbers (Gruber 1991; Calude and Zamfirescu 1998; Trott 2004, p. 69).

REFERENCES:

Borwein, J. and Borwein, P. A Dictionary of Real Numbers. Pacific Grove, CA: Brooks/Cole, 1990.

Calude, C. S. and Zamfirescu, T. "The Typical Number Is a Lexicon." New Zealand J. Math. 27, 7-13, 1998.

Gruber, P. M. "An Overview of the Geometry of Numbers Including Aspects of Construction and Computation." Rendiconti Sem. Mat. Messina Ser. II, 1, 21-28, 1991.

Jeffreys, H. and Jeffreys, B. S. "Real Numbers." §1.03 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 5-6, 1988.

Plouffe, S. "Plouffe's Inverter." https://pi.lacim.uqam.ca/eng/.

Shamos, M. I. A Catalog of Real Numbers. In preparation? https://www.ecom.cmu.edu/people/faculty/mshamos/resshort.htm

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. https://www.mathematicaguidebooks.org/.