Ramanujan Prime

The 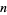th Ramanujan prime is the smallest number  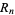such that  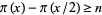for all 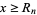, where  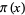is the prime counting function. In other words, there are at least  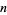primes between  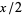and  whenever 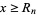. The smallest such number  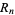must be prime, since the function  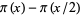can increase only at a prime.

Equivalently,

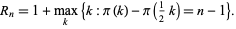Using simple properties of the gamma function, Ramanujan (1919) gave a new proof of Bertrand's postulate. Then he proved the generalization that 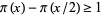, 2, 3, 4, 5, ... if 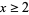, 11, 17, 29, 41, ... (OEIS A104272), respectively. These are the first few Ramanujan primes.

The case 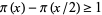 for all  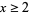is Bertrand's postulate.

REFERENCES:

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., pp. 208-209, 2000.

Ramanujan, S. "A Proof of Bertrand's Postulate." J. Indian Math. Soc. 11, 181-182, 1919.

Sloane, N. J. A. Sequence A104272 in "The On-Line Encyclopedia of Integer Sequences."