Wang's Conjecture

Wang's conjecture states that if a set of tiles can tile the plane, then they can always be arranged to do so periodically (Wang 1961). The conjecture was refuted when Berger (1966) showed that an aperiodic set of tiles existed. Berger used 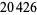 tiles, but the number has subsequently been greatly reduced. In fact, Culik (1996) has reduced the number of colored square tiles to 13.

For purely square tiles, Culik's record still stands as of Feb. 2009. For non-square tiles, it is much more complicated due to the Penrose tiles (2 tiles), the Robertson tiling (6 tiles), and various Ammann tilings (2-5 tiles).

REFERENCES:

Adler, A. and Holroyd, F. C. "Some Results on One-Dimensional Tilings." Geom. Dedicata 10, 49-58, 1981.

Berger, R. "The Undecidability of the Domino Problem." Mem. Amer. Math. Soc. No. 66, 1-72, 1966.

Culik, K. II "An Aperiodic Set of 13 Wang Tiles." Disc. Math. 160, 245-251, 1996.

Dutch, S. "Aperiodic Tilings." May 29, 2003. https://www.uwgb.edu/dutchs/symmetry/aperiod.htm.

Grünbaum, B. and Shephard, G. C. Tilings and Patterns. New York: W. H. Freeman, 1986.

Hanf, W. "Nonrecursive Tilings of the Plane. I." J. Symbolic Logic 39, 283-285, 1974.

Kari, J. "A Small Aperiodic Set of Wang Tiles." Disc. Math. 160, 259-264, 1996.

Mozes, S. "Tilings, Substitution Systems, and Dynamical Systems Generated by Them." J. Analyse Math. 53, 139-186, 1989.

Myers, D. "Nonrecursive Tilings of the Plane. II." J. Symbolic Logic 39, 286-294, 1974.

Radin, C. Miles of Tiles. Providence, RI: Amer. Math. Soc., pp. 6-8, 1999.

Robinson, R. M. "Undecidability and Nonperiodicity for Tilings of the Plane." Invent. Math. 12, 177-209, 1971.

Smith, T. "Penrose Tilings and Wang Tilings." https://www.innerx.net/personal/tsmith/pwtile.html.

Wang, H. "Proving Theorems by Pattern Recognition. II." Bell Systems Tech. J. 40, 1-41, 1961.