المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
حق مالك الضمان في الاحتفاظ بملكية العين المخصصة للضمان
2025-04-05
حق المالك في إيجار العين المخصصة للضمان
2025-04-05
Farsi (Samiian 1994; Ghomeshi 1997; Ghozati 2000; Kahnemuyipour 2000)
2025-04-05
The Ezafe construction
2025-04-05
Ezafe and the deep position on nominal modifiers Introduction
2025-04-05
الايمان عند الهلاك غير مقبول
2025-04-05

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
الأصل النقلي الاول للتفسير: القرآن الكريم
2024-09-06
تفسير قوله تعالى : {مالِكِ يَوْمِ الدِّينِ}
14-06-2015
مرض العفن الطري البكتيري Bacterial soft rot
2024-01-31
المماثلة
23-04-2015
deverbal (adj.)
2023-08-10
الشكر وكفران النعمة
2025-01-11

Gauss,s Continued Fraction  
  
873   04:32 مساءً   date: 30-4-2020
Author : Borwein, J.; Bailey, D.; and Girgensohn, R.
Book or Source : "Gauss,s Continued Fraction." §1.8.3 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters
Page and Part : ...


Read More
Theodorus,s Constant
Date: 26-7-2020 1005
Suzanne Set
Date: 7-11-2020 880
Sylvester Cyclotomic Number
Date: 7-11-2020 743

Gauss's Continued Fraction

Gauss's continued fraction is given by the continued fraction

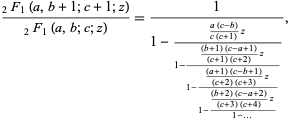(_2F_1(a,b+1;c+1;z))/(_2F_1(a,b;c;z))=1/(1-((a(c-b))/(c(c+1))z)/(1-(((b+1)(c-a+1))/((c+1)(c+2))z)/(1-(((a+1)(c-b+1))/((c+2)(c+3))z)/(1-(((b+2)(c-a+2))/((c+3)(c+4))z)/(1-...))))),

where 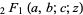_2F_1(a,b;c;z) is a hypergeometric function. Many analytic expressions for continued fractions of functions can be derived from this formula.

REFERENCES:

Borwein, J.; Bailey, D.; and Girgensohn, R. "Gauss's Continued Fraction." §1.8.3 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 31-34, 2004.

Wall, H. S. "The Continued Fraction of Gauss." Ch. 18 in Analytic Theory of Continued Fractions. New York: Chelsea, pp. 335-361, 1948.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
التاريخ / 2025-04-04

الأخبار العلمية
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
التاريخ / 2025-04-04

الساحة الاسلامية
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
التاريخ / 2025-04-05