


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-9-2020
Date: 27-10-2019
Date: 22-10-2019
|
Let two points 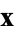 and
and 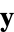 be picked randomly from a unit
be picked randomly from a unit 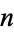 -dimensional hypercube. The expected distance between the points
-dimensional hypercube. The expected distance between the points 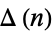 , i.e., the mean line segment length, is then
, i.e., the mean line segment length, is then
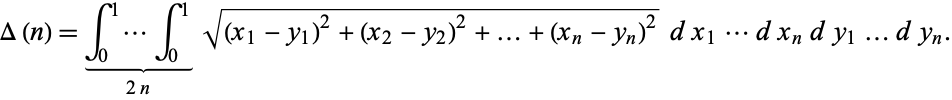 |
(1) |
This multiple integral has been evaluated analytically only for small values of 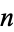 . The case
. The case 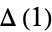 corresponds to the line line picking between two random points in the interval
corresponds to the line line picking between two random points in the interval ![[0,1]](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/Inline7.gif) .
.
The first few values for 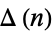 are given in the following table.
are given in the following table.
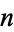 |
OEIS | 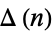 |
| 1 | -- | 0.3333333333... |
| 2 | A091505 | 0.5214054331... |
| 3 | A073012 | 0.6617071822... |
| 4 | A103983 | 0.7776656535... |
| 5 | A103984 | 0.8785309152... |
| 6 | A103985 | 0.9689420830... |
| 7 | A103986 | 1.0515838734... |
| 8 | A103987 | 1.1281653402... |
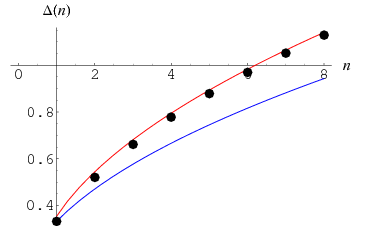
The function 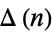 satisfies
satisfies
![1/3n^(1/2)<=Delta(n)<=(1/6n)^(1/2)sqrt(1/3[1+2(1-3/(5n))^(1/2)])](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/NumberedEquation2.gif) |
(2) |
(Anderssen et al. 1976), plotted above together with the actual values.
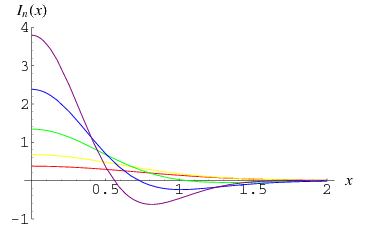
M. Trott (pers. comm., Feb. 23, 2005) has devised an ingenious algorithm for reducing the 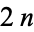 -dimensional integral to an integral over a 1-dimensional integrand
-dimensional integral to an integral over a 1-dimensional integrand 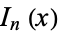 such that
such that
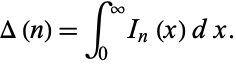 |
(3) |
The first few values are
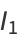 |
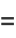 |
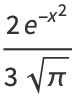 |
(4) |
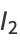 |
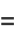 |
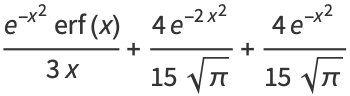 |
(5) |
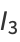 |
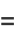 |
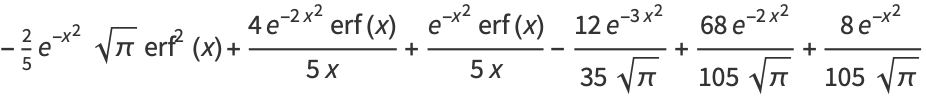 |
(6) |
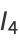 |
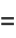 |
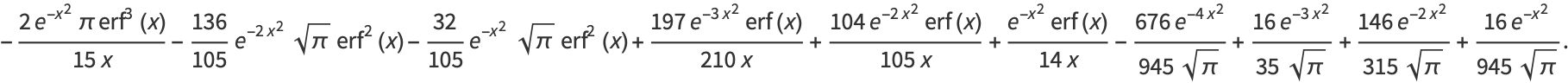 |
(7) |
In the limit as 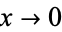 , these have values for
, these have values for 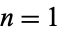 , 2, ... given by
, 2, ... given by 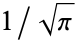 times 2/3, 6/5, 50/21, 38/9, 74/11, ... (OEIS A103990 and A103991).
times 2/3, 6/5, 50/21, 38/9, 74/11, ... (OEIS A103990 and A103991).
This is equivalent to computing the box integral
![Delta_n(s)=s/(Gamma(1-1/2s))int_0^infty(1-[d(u)]^n)/(u^(s+1))du](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/NumberedEquation4.gif) |
(8) |
where
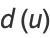 |
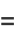 |
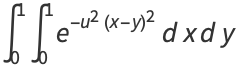 |
(9) |
 |
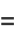 |
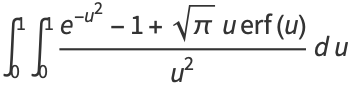 |
(10) |
(Bailey et al. 2006).
These give closed-form results for 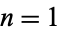 , 2, 3, and 4:
, 2, 3, and 4:
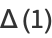 |
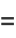 |
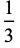 |
(11) |
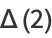 |
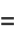 |
![1/(15)[sqrt(2)+2+5ln(1+sqrt(2))]](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/Inline41.gif) |
(12) |
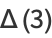 |
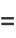 |
![1/(105)[4+17sqrt(2)-6sqrt(3)+21ln(1+sqrt(2))+42ln(2+sqrt(3))-7pi]](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/Inline44.gif) |
(13) |
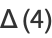 |
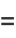 |
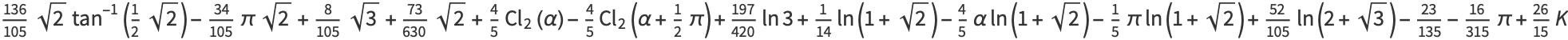 |
(14) |
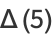 |
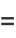 |
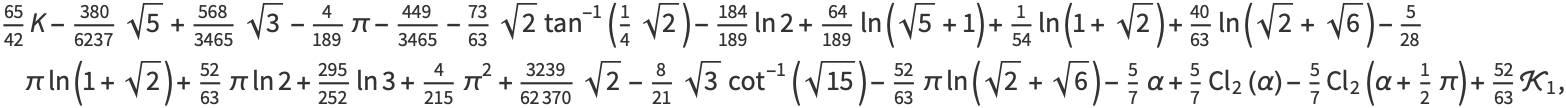 |
(15) |
where 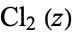 is a Clausen function,
is a Clausen function, 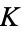 is Catalan's constant, and
is Catalan's constant, and
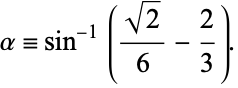 |
(16) |
The 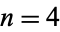 case above seems to be published here for the first time; the simplified form given above is due to Bailey et al. (2006). Attempting to reduce
case above seems to be published here for the first time; the simplified form given above is due to Bailey et al. (2006). Attempting to reduce 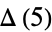 to quadratures gives closed-form pieces with the exception of the single piece
to quadratures gives closed-form pieces with the exception of the single piece
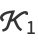 |
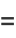 |
![pi[1/2ln(2+sqrt(3))-int_0^infty(e^(-2x^2)erf^3(x))/xdx]](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/Inline57.gif) |
(17) |
 |
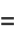 |
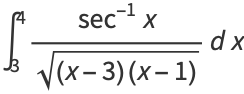 |
(18) |
 |
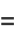 |
![int_0^(I[cos^(-1)2])sec^(-1)(2+coshtheta)dtheta](http://mathworld.wolfram.com/images/equations/HypercubeLinePicking/Inline63.gif) |
(19) |
which appears to be difficult to integrate in closed form (Bailey et al. 2007, p. 272).
The value 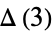 obtained for cube line picking is sometimes known as the Robbins constant.
obtained for cube line picking is sometimes known as the Robbins constant.
REFERENCES:
Anderssen, R. S.; Brent, R. P.; Daley, D. J.; and Moran, A. P. "Concerning 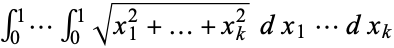 and a Taylor Series Method." SIAM J. Appl. Math. 30, 22-30, 1976.
and a Taylor Series Method." SIAM J. Appl. Math. 30, 22-30, 1976.
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "Box Integrals." Preprint. Apr. 3, 2006.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 272, 2007.
Finch, S. R. "Geometric Probability Constants." §8.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 479-484, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 30, 1983.
Robbins, D. "Average Distance between Two Points in a Box." Amer. Math. Monthly 85, 278, 1978.
Sloane, N. J. A. Sequences A073012, A091505, A103983, A103984, A103985, A103986, A103987, A103988, A103989, A103990, and A103991 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. "The Area of a Random Triangle." Mathematica J. 7, 189-198, 1998.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|