


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-3-2020
Date: 28-10-2020
Date: 1-1-2020
|
A cusp form is a modular form for which the coefficient 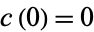 in the Fourier series
in the Fourier series
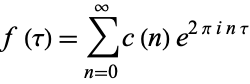 |
(1) |
(Apostol 1997, p. 114). The only entire cusp form of weight 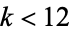 is the zero function (Apostol 1997, p. 116). The set of all cusp forms in
is the zero function (Apostol 1997, p. 116). The set of all cusp forms in 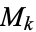 (all modular forms of weight
(all modular forms of weight 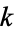 ) is a linear subspace of
) is a linear subspace of 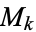 which is denoted
which is denoted 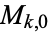 . The dimension of
. The dimension of 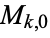 is 1 for
is 1 for 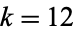 , 16, 18, 20, 22, and 26 (Apostol 1997, p. 119). For a cusp form
, 16, 18, 20, 22, and 26 (Apostol 1997, p. 119). For a cusp form 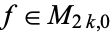 ,
,
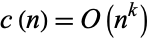 |
(2) |
(Apostol 1997, p. 135) or, more precisely,
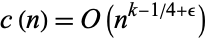 |
(3) |
for every 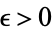 (Selberg 1965; Apostol 1997, p. 136). It is conjectured that the
(Selberg 1965; Apostol 1997, p. 136). It is conjectured that the 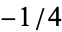 in the exponent can be reduced to
in the exponent can be reduced to 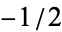 (Apostol 1997, p. 136).
(Apostol 1997, p. 136).
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 114 and 116, 1997.
Selberg, A. "On the Estimate of Coefficients of Modular Forms." Proc. Sympos. Pure Math. 8, 1-15, 1965.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|