Sign

Min   Max       Re       Im

The sign of a real number, also called sgn or signum, is 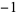 for a negative number (i.e., one with a minus sign "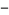"), 0 for the number zero, or  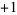for a positive number (i.e., one with a plus sign "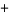"). In other words, for real ,

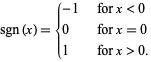(1)

For real 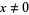, this can be written

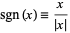(2)

and satisfies

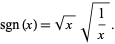(3)

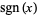 for real  can also be defined as

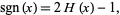(4)

where 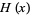 is the Heaviside step function.

The sign function is implemented in the Wolfram Language for real  as Sign[x]. For nonzero complex numbers, Sign[z] returns 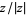, where  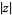is the complex modulus of .

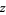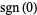 can also be interpreted as an unspecified point on the unit circle in the complex plane (Rich and Jeffrey 1996).

REFERENCES:

Bracewell, R. "The Sign Function, 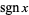." In The Fourier Transform and Its Applications, 3rd ed. New York: McGraw-Hill, pp. 61-62, 1999.

Rich, A. and Jeffrey, D. "Function Evaluation on Branch Cuts." SIGSAM Bull., No. 116, 25-27, June 1996.