
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-6-2020
Date: 7-10-2020
Date: 13-1-2021
|
Synthetic division is a shortcut method for dividing two polynomials which can be used in place of the standard long division algorithm. This method reduces the dividend and divisor polynomials into a set of numeric values. After these values are processed, the resulting set of numeric outputs is used to construct the polynomial quotient and the polynomial remainder.
For an example of synthetic division, consider dividing 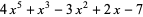 by
by 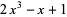 . First, if a power of
. First, if a power of  is missing from either polynomial, a term with that power and a zero coefficient must be inserted into the correct position in the respective polynomial. In this case the
is missing from either polynomial, a term with that power and a zero coefficient must be inserted into the correct position in the respective polynomial. In this case the  term is missing from the dividend while the
term is missing from the dividend while the 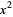 term is missing from the divisor; therefore,
term is missing from the divisor; therefore, 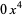 is added between the quintic and the cubic terms of the dividend while
is added between the quintic and the cubic terms of the dividend while 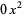 is added between the cubic and the linear terms of the divisor:
is added between the cubic and the linear terms of the divisor:
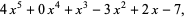 |
(1) |
and
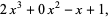 |
(2) |
respectively.
Next, all the variables and their exponents (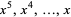 ) are removed from the dividend, leaving instead a list consisting solely of its coefficients:
) are removed from the dividend, leaving instead a list consisting solely of its coefficients: 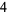 ,
, 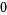 ,
, 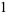 ,
, 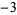 ,
, 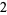 , and
, and 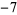 . This sequence of numbers is placed into a division-like configuration:
. This sequence of numbers is placed into a division-like configuration:

Variables are then similarly removed from the divisor, yielding a sequence 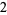 ,
, 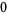 ,
, 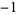 , and
, and 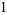 . Because the divisor fails to be monic, one must keep track of the leading coefficient (
. Because the divisor fails to be monic, one must keep track of the leading coefficient (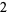 in this case); after doing so, the divisor's leading coefficient is discarded and the signs of its remaining coefficients are "reversed," thereby leaving a "modified sequence" of
in this case); after doing so, the divisor's leading coefficient is discarded and the signs of its remaining coefficients are "reversed," thereby leaving a "modified sequence" of 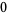 ,
, 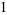 , and
, and 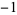 corresponding to the divisor. This modified sequence, along with the leading coefficient, are filled into the above-shown division-like configuration as follows:
corresponding to the divisor. This modified sequence, along with the leading coefficient, are filled into the above-shown division-like configuration as follows:

The first number in the dividend (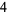 in this case) is put into the first position of the first result area (i.e., the first row below the horizontal line). This number is the coefficient of the
in this case) is put into the first position of the first result area (i.e., the first row below the horizontal line). This number is the coefficient of the 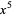 term in the original dividend polynomial:
term in the original dividend polynomial:
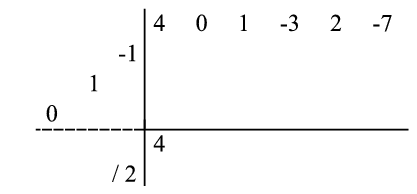
At this point, it is imperative that the leading coefficient of the divisor be recognized; before continuing, the first number of the dividend (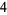 ) must be divided by this leading coefficient (
) must be divided by this leading coefficient (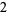 ), the result of which (
), the result of which (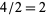 ) will be recorded into the first position of the second result area (i.e., the second row below the horizontal line). This number is "modified coefficient" of the
) will be recorded into the first position of the second result area (i.e., the second row below the horizontal line). This number is "modified coefficient" of the 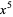 term in the original dividend after it is been divided by the leading coefficient of the divisor:
term in the original dividend after it is been divided by the leading coefficient of the divisor:
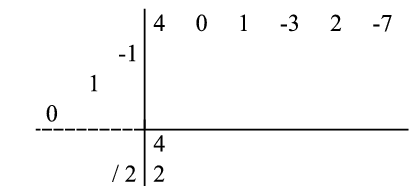
Now, the first entry in this latest result (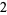 ) is multiplied by each element of the coefficient sequence from the divisor (
) is multiplied by each element of the coefficient sequence from the divisor (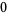 ,
, 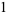 , and
, and 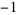 ), the products of which are placed diagonally under the next dividend terms as follows:
), the products of which are placed diagonally under the next dividend terms as follows:
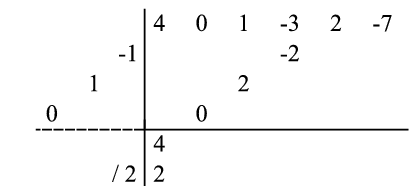
As the algorithm progresses, the numbers from the dividend are added systematically to the results of the multiplications performed; in particular, this addition happens when the resulting product element is directly above the horizontal line. The result of the addition is placed on the first result line:
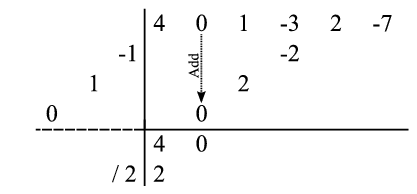
At this point, the process essentially repeats: The last-dropped number from the first result line (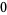 in this case) is divided by the leading coefficient of the divisor (
in this case) is divided by the leading coefficient of the divisor (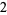 ) to yield a number (
) to yield a number (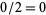 here) placed on the second result line:
here) placed on the second result line:
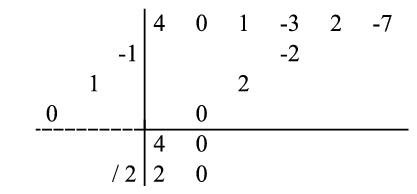
This result (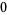 ) is multiplied by the left-hand divisor sequence (
) is multiplied by the left-hand divisor sequence (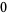 ,
, 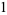 , and
, and 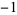 ) to yield products (
) to yield products (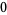 ,
, 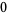 , and
, and 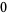 ) which are placed diagonally under the subsequent dividend terms:
) which are placed diagonally under the subsequent dividend terms:
Next comes addition along the subsequent column (the 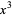 dividend column, here consisting of
dividend column, here consisting of 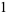 ,
, 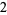 , and
, and 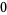 ), the result of which (
), the result of which (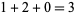 in this case) is divided by the leading divisor coefficient (
in this case) is divided by the leading divisor coefficient (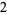 ) to yield a result of
) to yield a result of 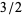 :
:
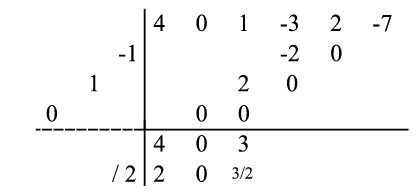
Finally, the process repeats: 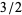 is multiplied by the sequence
is multiplied by the sequence 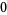 ,
, 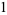 ,
, 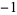 to yield the sequence
to yield the sequence 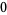 ,
, 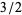 ,
, 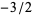 which again is placed diagonally beneath the corresponding dividend terms:
which again is placed diagonally beneath the corresponding dividend terms:
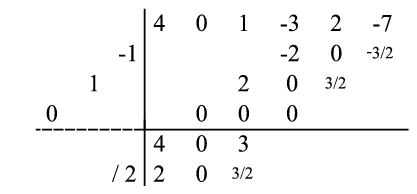
Adding the subsequent column (the 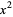 dividend column consisting of
dividend column consisting of 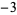 ,
, 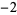 ,
, 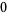 ,
, 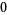 ) yields a result (namely,
) yields a result (namely, 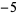 ), and because any subsequent collections of products would consist of more numbers (namely,
), and because any subsequent collections of products would consist of more numbers (namely, 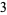 numbers, one for each of the three left-hand sequence numbers) than there are dividend terms remaining (there are two such terms, namely the
numbers, one for each of the three left-hand sequence numbers) than there are dividend terms remaining (there are two such terms, namely the  -coefficient of
-coefficient of 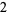 and the constant,
and the constant, 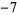 ), no additional products are required. Hence, this result (
), no additional products are required. Hence, this result (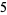 ) need not be divided by the leading divisor coefficient (
) need not be divided by the leading divisor coefficient (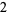 ), whereby the remaining columns may be summed without division. This final step can be diagrammed as follows:
), whereby the remaining columns may be summed without division. This final step can be diagrammed as follows:
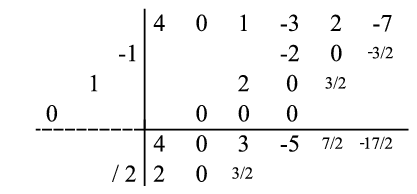
The result is the list of six numbers (the leftmost three from the second result row and the rightmost three from the first result row), namely
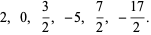 |
(3) |
In order to determine which of these numbers become the coefficients of the quotient polynomial, first determine how many numbers were in the left-hand sequence. Because this sequence consists of three numbers (namely, 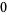 ,
, 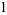 , and
, and 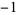 ), the first three numbers (namely
), the first three numbers (namely 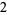 ,
, 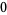 , and
, and 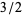 ) of the sequence (3) will be coefficients of the quotient polynomial
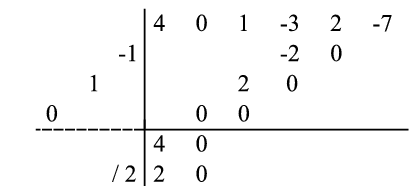
) of the sequence (3) will be coefficients of the quotient polynomial 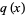 , a polynomial which will be quadratic due to the fact that a quintic was divided by a cubic. Hence, the quotient polynomial has the form:
, a polynomial which will be quadratic due to the fact that a quintic was divided by a cubic. Hence, the quotient polynomial has the form:
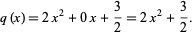 |
(4) |
Moreover, the remaining numbers (namely, 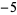 ,
, 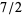 , and
, and 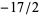 ) of (3) correspond to the coefficients of the remainder polynomial
) of (3) correspond to the coefficients of the remainder polynomial 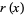 ; here,
; here,
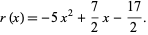 |
(5) |
The quotient and remainder can be combined into a single expression:
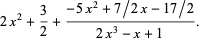 |
(6) |
Note, too, that the only division operations performed during this computation consisted of dividing entries from the first result row by the leading divisor coefficient 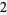 , whereby it follows that the quotient (6) was computed after performing only three divisions.
, whereby it follows that the quotient (6) was computed after performing only three divisions.
Unsurprisingly, this process can be verified:
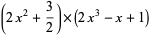 |
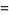 |
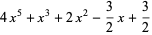 |
(7) |
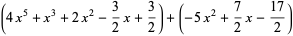 |
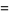 |
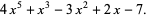 |
(8) |
In particular, multiplying the quotient by the divisor and adding the remainder yields the original dividend polynomial, thus confirming the validity of the result.
The process described above is perhaps the most general case of synthetic division of univariate polynomials; as such, it is sometimes referred to as generalized synthetic division, expanded synthetic division, or generalized expanded synthetic division. Although confusing, the special case in which the divisor is a monic polynomial of arbitrary degree (no more than the degree of the dividend) is sometimes referred to as expanded synthetic division, while the case most often referred to by the unqualified term "synthetic division" consists of a monic linear divisor and is more formally referred to as Ruffini's Rule.
REFERENCES:
Fan, L. "A Generalization of Synthetic Division and a General Theorem of Division of Polynomials." Mathematical Medley 30, 30-37, 2003. http://eprints.soton.ac.uk/168861/1/FLH_article_on_polynomial_division.pdf.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|