Jacobsthal Polynomial

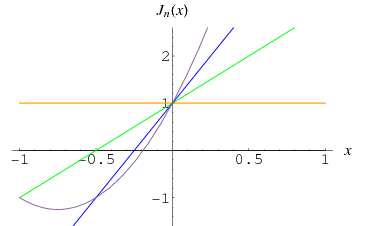
The Jacobsthal polynomials are the -polynomial obtained by setting 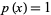 and 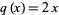 in the Lucas polynomial sequence. The first few Jacobsthal polynomials are

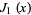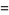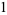			(1)
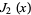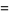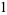			(2)
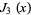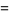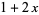			(3)
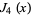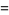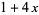			(4)
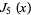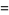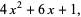			(5)

Jacobsthal polynomials satisfy

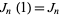(6)

where 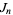 is a Jacobsthal number.

REFERENCES:

Djordjevic, G. B. "Jacobsthal Polynomials." Fib. Quart. 38, 239, 2000.

Filipponi, P. and Horadam, A. F. "Jacobsthal and Jacobsthal-Lucas Polynomials." Proc. Int. Conf. Fib. Numb. Appl., Vol. 8, p. 129, 1999.

Hoggatt, V. E. Jr. and Bicknell-Johnson, M. "Arrays for Jacobsthal and Fibonacci Polynomials." bf 16, 385, 1978.

Horadam, A. F. and Filipponi, P. "Fibonacci and Lucas Polynomials." Proc. Int. Conf. Fib. Numb. Appl., Vol. 5, p. 317, 1993.

Jacobsthal, P. "Fibonaccische Polynome und Kreisteilungsgleichungen." Sitzungsber. Berliner Math. Gesell. 17, 43-57, 1919-1920.

Swamy, M. N. S. "Jacobsthal Polynomials, A." Fib. Quart. 37, 141, 1999.