


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-4-2019
Date: 21-9-2018
Date: 2-5-2019
|
The q-analog of the Pochhammer symbol defined by
 |
(1) |
(Koepf 1998, p. 25).  -Pochhammer symbols are frequently called q-series and, for brevity,
-Pochhammer symbols are frequently called q-series and, for brevity, 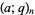 is often simply written
is often simply written 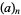 . Note that this contention has the slightly curious side-effect that the argument is not taken literally, so for example
. Note that this contention has the slightly curious side-effect that the argument is not taken literally, so for example 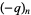 means
means 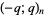 , not
, not 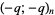 (cf. Andrews 1986b).
(cf. Andrews 1986b).
The 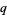 -Pochhammer symbol
-Pochhammer symbol 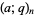 is implemented in the Wolfram Language as QPochhammer[a, q, n], with the special cases
is implemented in the Wolfram Language as QPochhammer[a, q, n], with the special cases 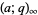 and
and 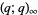 represented as QPochhammer[a, q] and QPochhammer[q], respectively.
represented as QPochhammer[a, q] and QPochhammer[q], respectively.
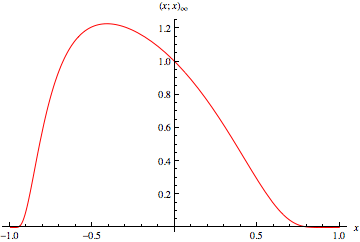 |
 |
Letting  gives the special case
gives the special case  , sometimes known as "the" Euler function
, sometimes known as "the" Euler function 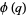 and defined by
and defined by
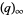 |
 |
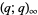 |
(2) |
 |
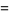 |
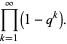 |
(3) |
This function is closely related to the pentagonal number theorem and other related and beautiful sum/product identities. As mentioned above, it is implemented in Mathematica as QPochhammer[q]. As can be seen in the plot above, along the real axis, 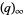 reaches a maximum value
reaches a maximum value 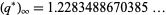 (OEIS A143440) at value
(OEIS A143440) at value 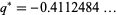 (OEIS A143441).
(OEIS A143441).
The general 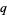 -Pochhammer symbol is given by the sum
-Pochhammer symbol is given by the sum
![sum_(k=0)^n(-a)^kq^((k; 2))[n; k]_q=(a;q)_n,](http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/NumberedEquation2.gif) |
(4) |
where ![[n; k]_q](http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/Inline24.gif) is a q-binomial coefficient (Koekoek and Swarttouw 1998, p. 11).
is a q-binomial coefficient (Koekoek and Swarttouw 1998, p. 11).
It is closely related to the Dedekind eta function,
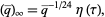 |
(5) |
where  the half-period ratio and
the half-period ratio and 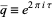 is the square of the nome (Berndt 1994, p. 139). Other representations in terms of special functions include
is the square of the nome (Berndt 1994, p. 139). Other representations in terms of special functions include
 |
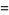 |
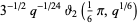 |
(6) |
 |
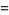 |
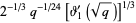 |
(7) |
where 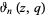 is a Jacobi theta function (and in the latter case, care must be taken with the definition of the principal value the cube root).
is a Jacobi theta function (and in the latter case, care must be taken with the definition of the principal value the cube root).
Asymptotic results for  -Pochhammer symbols include
-Pochhammer symbols include
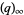 |
 |
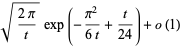 |
(8) |
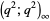 |
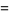 |
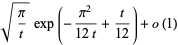 |
(9) |
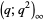 |
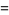 |
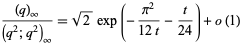 |
(10) |
for 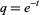 (Watson 1936, Gordon and McIntosh 2000).
(Watson 1936, Gordon and McIntosh 2000).
For 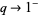 ,
,
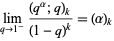 |
(11) |
gives the normal Pochhammer symbol 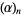 (Koekoek and Swarttouw 1998, p. 7). The
(Koekoek and Swarttouw 1998, p. 7). The 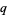 -Pochhammer symbols are also called
-Pochhammer symbols are also called 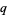 -shifted factorials (Koekoek and Swarttouw 1998, pp. 8-9).
-shifted factorials (Koekoek and Swarttouw 1998, pp. 8-9).
The 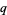 -Pochhammer symbol satisfies
-Pochhammer symbol satisfies
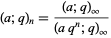 |
(12) |
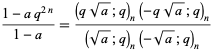 |
(13) |
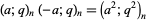 |
(14) |
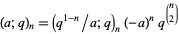 |
(15) |
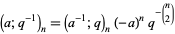 |
(16) |
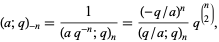 |
(17) |
(here, 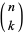 is a binomial coefficient so
is a binomial coefficient so 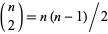 ), as well as many other identities, some of which are given by Koekoek and Swarttouw (1998, p. 9).
), as well as many other identities, some of which are given by Koekoek and Swarttouw (1998, p. 9).
A generalized 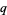 -Pochhammer symbol can be defined using the concise notation
-Pochhammer symbol can be defined using the concise notation
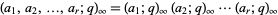 |
(18) |
(Gordon and McIntosh 2000).
The 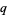 -bracket
-bracket
![[n]_q=[n; 1]_q](http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/NumberedEquation12.gif) |
(19) |
and 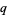 -binomial
-binomial
![[n]_q!=product_(k=1)^n[k]_q](http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/NumberedEquation13.gif) |
(20) |
symbols are sometimes also used when discussing 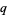 -series, where
-series, where ![[n; 1]_q](http://mathworld.wolfram.com/images/equations/q-PochhammerSymbol/Inline56.gif) is a
is a 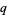 -binomial coefficient.
-binomial coefficient.
REFERENCES:
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., 1986a.
Andrews, G. E. "The Fifth and Seventh Order Mock Theta Functions." Trans. Amer. Soc. 293, 113-134, 1986b.
Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, 1998.
Andrews, G. E.; Askey, R.; and Roy, R. Special Functions. Cambridge, England: Cambridge University Press, 1999.
Berndt, B. C. "q-Series." Ch. 27 in Ramanujan's Notebooks, Part IV. New York:Springer-Verlag, pp. 261-286, 1994.
Berndt, B. C.; Huang, S.-S.; Sohn, J.; and Son, S. H. "Some Theorems on the Rogers-Ramanujan Continued Fraction in Ramanujan's Lost Notebook." Trans. Amer. Math. Soc. 352, 2157-2177, 2000.
Bhatnagar, G. "A Multivariable View of One-Variable q-Series." In Special Functions and Differential Equations. Proceedings of the Workshop (WSSF97) held in Madras, January 13-24, 1997) (Ed. K. S. Rao, R. Jagannathan, G. van den Berghe, and J. Van der Jeugt). New Delhi, India: Allied Pub., pp. 60-72, 1998.
Gasper, G. "Lecture Notes for an Introductory Minicourse on 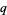 -Series." 25 Sep 1995. http://arxiv.org/abs/math.CA/9509223.
-Series." 25 Sep 1995. http://arxiv.org/abs/math.CA/9509223.
Gasper, G. "Elementary Derivations of Summation and Transformation Formulas for q-Series." In Fields Inst. Comm. 14 (Ed. M. E. H. Ismail et al. ), pp. 55-70, 1997.
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, 1990.
Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.
Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 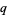 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, p. 7, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 25 and 30, 1998.
Sloane, N. J. A. Sequences A143440 and A143441 in "The On-Line Encyclopedia of Integer Sequences."Watson, G. N. "The Final Problem: An Account of the Mock Theta Functions." J. London Math. Soc. 11, 55-80, 1936.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|