المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Rosenbrock Function |
 1113
 05:01 مساءً
date: 23-7-2019 |
Author : Germundsson, R. 
Book or Source : "Mathematica Version 4." Mathematica J. 7 
Page and Part : ...|
Read More
Date: 15-5-2018
2010
Date: 21-7-2019
1452
Date: 12-8-2018
1469
|
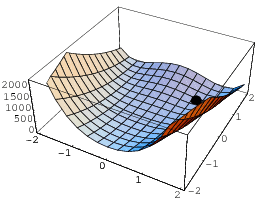
The function
 |
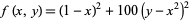that is often used as a test problem for optimization algorithms (where a variation with 100 replaced by 105 is sometimes used; Germundsson 2000). It has a global minimum of 0 at the point (1, 1).
REFERENCES:
Germundsson, R. "Mathematica Version 4." Mathematica J. 7, 497-524, 2000.
Rosenbrock, H. H. "An Automatic Method for Finding the Greatest or Least Value of a Function." Computer J. 3, 175-184, 1960.
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
جامعة الكفيل: كلية الطب توفّر نظامًا تعليميًّا يواكب التطور العالمي في المجال الطبي
|
|
|
