المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Trigamma Function |
 2439
 12:07 صباحاً
date: 23-5-2019 |
Author : Jeffreys, H. and Jeffreys, B. S. 
Book or Source : "The Digamma (F) and Trigamma () Functions." Methods of Mathematical Physics, 3rd ed.Cambridge, England: Cambridge University Press 
Page and Part : pp. 465-466|
Read More
Date: 12-10-2018
3208
Date: 25-8-2018
2113
Date: 15-6-2019
3063
|
 |
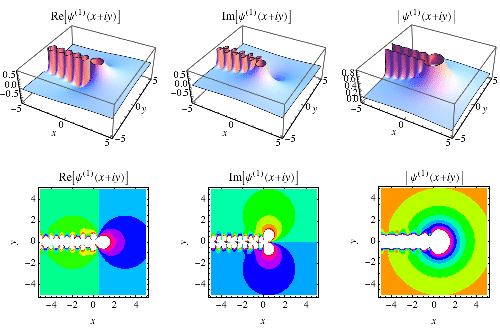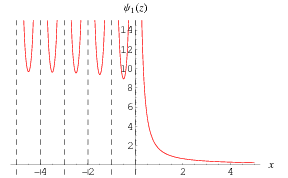
A special function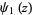 
corresponding to a polygamma function 
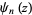with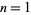 
, given by
 |
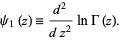(1) |
An alternative function
 |
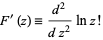(2) |
is sometimes called the trigamma function, where
 |
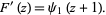(3) |
Sums and differences of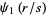 
for small integral 
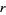and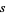 
can be expressed in terms of Catalan's constant 
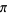and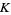 
. For example,
 |
 |
 |
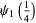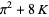(4) |
 |
 |
 |
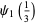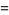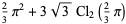(5) |
 |
 |
 |
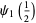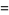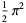(6) |
 |
 |
 |
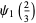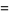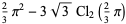(7) |
 |
 |
 |
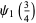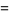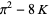(8) |
 |
 |
 |
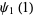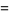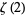(9) |
 |
 |
 |
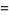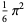(10) |
 |
 |
 |
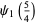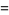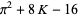(11) |
 |
 |
 |
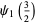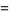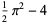(12) |
 |
 |
 |
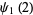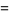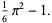(13) |
REFERENCES:
Jeffreys, H. and Jeffreys, B. S. "The Digamma (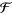
) and Trigamma (
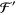) Functions." Methods of Mathematical Physics, 3rd ed.Cambridge, England: Cambridge University Press, pp. 465-466, 1988.
|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|
