Sparse Polynomial Square

A sparse polynomial square is a square of a polynomial  that has fewer terms than the original polynomial 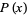. Examples include Rényi's polynomial

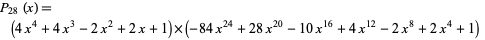(1)

(Rényi 1947, Coppersmith and Davenport 1991), which has 29 terms and whose square has 28, Choudhry's polynomial

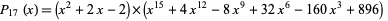(2)

(Coppersmith and Davenport 1991), which has 18 terms and whose square has 17, and

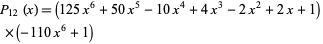(3)

(Coppersmith and Davenport 1991; Trott 2004, p. 276), which has 13 terms and whose square has 12.

In fact, Coppersmith and Davenport (1991) found eight polynomials of degree 13 having sparse squares (of degree 12),

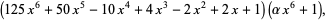(4)

where six of the 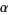 values are rational: 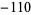, , 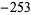, , 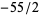, 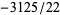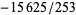and 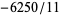 (Abbott 2002). Using Gröbner bases, Abbott (2002) showed that no polynomial of degree less than 12 has a sparse square, but was not able to demonstrate that these examples are exhaustive.

REFERENCES:

Abbott, J. "Sparse Squares of Polynomials." Math. Comput. 71, 407-413, 2002.

Coppersmith, D. and Davenport, J. "Polynomials Whose Powers Are Sparse." Acta Arith. 58, 79-87, 1991.

Erdős, P. "On the Number of Terms of the Square of a Polynomial." Nieuw Arch. Wisk. 23, 63-65, 1949.

Freud, R. "On the Minimum Number of Terms in the Square of a Polynomial." Mat. Lapok 24, 95-98, 1973.

Rényi, A. "On the Minimal Number of Terms in the Square of a Polynomial." Acta Math. Hungar. 1, 30-34, 1947. Reprinted in Selected Papers of Alfred Rényi, Vol. 1. Budapest, pp. 44-47, 1976.

Schinzel, A. "On the Number of Terms of a Power of a Polynomial." Acta Arith. 49, 55-70, 1987.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.

Verdenius, W. "On the Number of Terms of the Square and the Cube of Polynomials." Indag. Math. 11, 546-565, 1949.