
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-3-2017
Date: 17-2-2019
Date: 8-3-2017
|
Polynomial identities involving sums and differences of like powers include
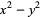 |
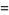 |
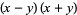 |
(1) |
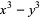 |
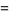 |
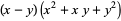 |
(2) |
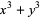 |
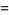 |
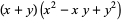 |
(3) |
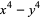 |
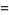 |
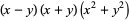 |
(4) |
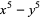 |
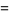 |
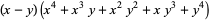 |
(5) |
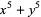 |
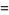 |
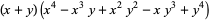 |
(6) |
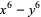 |
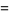 |
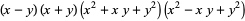 |
(7) |
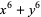 |
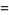 |
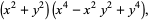 |
(8) |
which are the polynomial versions of the so-called binomial numbers.
Further identities include
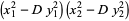 |
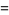 |
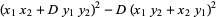 |
(9) |
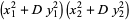 |
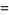 |
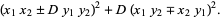 |
(10) |
The identity
![(X+Y+Z)^7-(X^7+Y^7+Z^7)=7(X+Y)(X+Z)(Y+Z)[(X^2+Y^2+Z^2+XY+XZ+YZ)^2+XYZ(X+Y+Z)]](http://mathworld.wolfram.com/images/equations/PolynomialIdentity/NumberedEquation1.gif) |
(11) |
was used by Lamé in his proof that Fermat's last theorem was true for 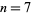 .
.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|