Laurent Polynomial

A Laurent polynomial with coefficients in the field 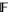 is an algebraic object that is typically expressed in the form

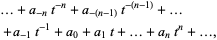where the 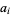 are elements of 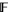, and only finitely many of the  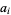are nonzero. A Laurent polynomial is an algebraic object in the sense that it is treated as a polynomial except that the indeterminant "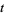" can also have negative powers.

Expressed more precisely, the collection of Laurent polynomials with coefficients in a field 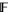 form a ring, denoted , with ring operations given by componentwise addition and multiplication according to the relation

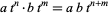for all 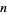 and 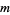 in the integers. Formally, this is equivalent to saying that  is the group ring of the integers and the field 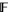. This corresponds to  (the polynomial ring in one variable for 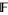) being the group ring or monoid ring for the monoid of natural numbers and the field .

REFERENCES:

Lang, S. Undergraduate Algebra, 2nd ed. New York: Springer-Verlag, 1990.