


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-12-2018
Date: 18-10-2018
Date: 27-11-2018
|
The generalized hypergeometric function is given by a hypergeometric series, i.e., a series for which the ratio of successive terms can be written
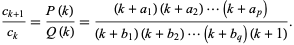 |
(1) |
(The factor of 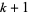 in the denominator is present for historical reasons of notation.) The resulting generalized hypergeometric function is written
in the denominator is present for historical reasons of notation.) The resulting generalized hypergeometric function is written
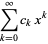 |
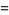 |
![_pF_q[a_1,a_2,...,a_p; b_1,b_2,...,b_q;x]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/Inline4.gif) |
(2) |
 |
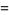 |
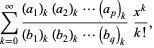 |
(3) |
where 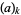 is the Pochhammer symbol or rising factorial
is the Pochhammer symbol or rising factorial
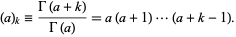 |
(4) |
A generalized hypergeometric function 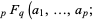
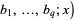 therefore has
therefore has 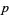 parameters of type 1 and
parameters of type 1 and 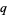 parameters of type 2.
parameters of type 2.
A number of generalized hypergeometric functions has special names. 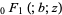 is called a confluent hypergeometric limit function, and is implemented in the Wolfram Language as Hypergeometric0F1[b, z].
is called a confluent hypergeometric limit function, and is implemented in the Wolfram Language as Hypergeometric0F1[b, z]. 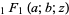 (also denoted
(also denoted 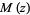 ) is called a confluent hypergeometric function of the first kind, and is implemented in the Wolfram Language as Hypergeometric1F1[a, b, z]. The function
) is called a confluent hypergeometric function of the first kind, and is implemented in the Wolfram Language as Hypergeometric1F1[a, b, z]. The function 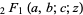 is often called "the" hypergeometric function or Gauss's hypergeometric function, and is implemented in the Wolfram Language as Hypergeometric2F1[a, b, c, x]. Arbitrary generalized hypergeometric functions are implemented as HypergeometricPFQ[
is often called "the" hypergeometric function or Gauss's hypergeometric function, and is implemented in the Wolfram Language as Hypergeometric2F1[a, b, c, x]. Arbitrary generalized hypergeometric functions are implemented as HypergeometricPFQ[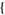 a1, ...ap
a1, ...ap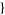 ,
, 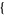 b1, ..., bq
b1, ..., bq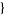 , x].
, x].
The notation for generalized hypergeometric functions was introduced by Pochhammer in 1870 and modified by Barnes (1907, 1908ab; Slater 1960, p. 2; Hardy 1999, p. 111). A number of notational variations are commonly used, including
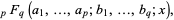 |
(5) |
used primarily for 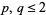 , using square brackets instead of parentheses
, using square brackets instead of parentheses
![_pF_q[a_1,...,a_p;b_1,...,b_q;x]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation4.gif) |
(6) |
(Slater 1960, p. 2), including  at the end of the first row and aligning slots in the second row from the right
at the end of the first row and aligning slots in the second row from the right
![_pF_q[a_1,a_2,...,a_p;; b_1,...,b_q z; ]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation5.gif) |
(7) |
(Bailey 1935, p. 9), including  at the end of the first row and centering each row
at the end of the first row and centering each row
![_pF_q[a_1,a_2,...,a_p;z; b_1,...,b_q]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation6.gif) |
(8) |
(Bailey 1935, p. 14), using strict matrix-like alignment of each column with columns right-aligned along their right-most elements
![_pF_q[a_1 a_2 ... a_p;; b_1 ..., b_q z; ]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation7.gif) |
(9) |
or
![_pF_q[a_1 a_2 ... a_p;; b_1 ..., b_q;z]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation8.gif) |
(10) |
(Slater 1960, p. 31), and a variation in which rows are centered and  is placed to the right separated by a vertical bar and using parenthesis
is placed to the right separated by a vertical bar and using parenthesis
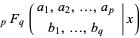 |
(11) |
(Graham et al. 1994, p. 205) or using square brackets and a semicolon
![_pF_q[a_1,a_2,...,a_p; b_1,...,b_q;x].](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation10.gif) |
(12) |
The latter convention will be used in this work, as it provides the clearest delineation of the argument  while making the most sparing use of white space in the typesetting of expressions that may contain a large number of symbolic parameters of differing lengths.
while making the most sparing use of white space in the typesetting of expressions that may contain a large number of symbolic parameters of differing lengths.
If the argument is equal to 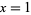 , then it is conventional to omit the argument altogether, although the trailing semicolon may be either retained or also discarded depending on notational convention. Bailey (1935, p. 9) uses the notation
, then it is conventional to omit the argument altogether, although the trailing semicolon may be either retained or also discarded depending on notational convention. Bailey (1935, p. 9) uses the notation
![_pF_q[a_1,a_2,...,a_p;; b_1,...,b_q]=_pF_q[a_1,a_2,...,a_p;1; b_1,b_2,...,b_q],](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation11.gif) |
(13) |
although in this work, the semicolon will be omitted, i.e.,
![_pF_q[a_1,a_2,...,a_p; b_1,b_2,...,b_q]=_pF_q[a_1,a_2,...,a_p; b_1,b_2,...,b_q].](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation12.gif) |
(14) |
The Kampe de Feriet function is a generalization of the generalized hypergeometric function to two variables.
The generalized hypergeometric function ![F_n(x)=_pF_q[a_1,a_2...,a_p; b_1,b_2,...,b_q;x]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/Inline27.gif) satisfies
satisfies
![thetaF_n(x)=n[F_(n+1)(x)-F_n(x)]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation13.gif) |
(15) |
for any of its numerator parameters 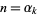 , and
, and
![thetaF_n(x)=(n-1)[F_(n-1)(x)-F_n(x)]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation14.gif) |
(16) |
for any of its denominator parameters 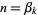 , where
, where
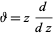 |
(17) |
is the differential operator (Rainville 1971, Koepf 1998, p. 27).
The generalized hypergeometric function
![_(p+1)F_p[a_1,a_2,...,a_(p+1); b_1,b_2,...,b_p;z]](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation16.gif) |
(18) |
is a solution to the differential equation
![[theta(theta+b_1-1)...(theta+b_p-1)-z(theta+a_1)(theta+a_2)...(theta+a_(p+1))]y=0](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation17.gif) |
(19) |
(Bailey 1935, p. 8). The other linearly independent solution is
![z^(1-b_1)_(p+1)F_p[1+a_1-b_1,1-a_2-b_2,...,1+a_(p+1)-b_1; 2-b_1,1-b_2-b_1,...,1-b_p-b_1;z].](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation18.gif) |
(20) |
A generalized hypergeometric function 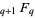 converges absolutely on the unit circle if
converges absolutely on the unit circle if
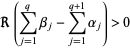 |
(21) |
(Rainville 1971, Koepf 1998).
Many sums can be written as generalized hypergeometric functions by inspection of the ratios of consecutive terms in the generating hypergeometric series. For example, for
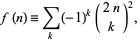 |
(22) |
the ratio of successive terms is
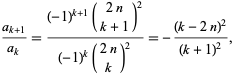 |
(23) |
yielding
![f(n)=_2F_1[-2n,-2n; 1;-1]=_2F_1(-2n,-2n;1;-1)](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation22.gif) |
(24) |
(Petkovšek et al. 1996, pp. 44-45).
Gosper (1978) discovered a slew of unusual hypergeometric function identities, many of which were subsequently proven by Gessel and Stanton (1982). An important generalization of Gosper's technique, called Zeilberger's algorithm, in turn led to the powerful machinery of the Wilf-Zeilberger pair (Zeilberger 1990).
Special hypergeometric identities include Gauss's hypergeometric theorem
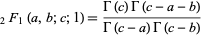 |
(25) |
for ![R[c-a-b]>0](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/Inline31.gif) , Kummer's formula
, Kummer's formula
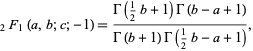 |
(26) |
where 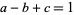 and
and 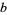 is a positive integer, Saalschütz's theorem
is a positive integer, Saalschütz's theorem
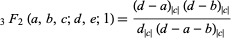 |
(27) |
for 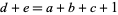 with
with 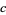 a negative integer and
a negative integer and 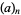 the Pochhammer symbol, Dixon's theorem
the Pochhammer symbol, Dixon's theorem
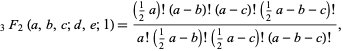 |
(28) |
where 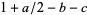 has a positive real part,
has a positive real part, 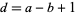 , and
, and 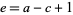 , the Clausen formula
, the Clausen formula
![_4F_3[a,b,c,d; e,f,g;1]=((2a)_(|d|)(a+b)_(|d|)(2b)_(|d|))/((2a+2b)_(|d|)a_(|d|)b_(|d|)),](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation27.gif) |
(29) |
for 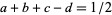 ,
, 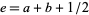 ,
, 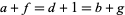 ,
, 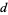 a nonpositive integer, and the Dougall-Ramanujan identity
a nonpositive integer, and the Dougall-Ramanujan identity
![_7F_6[a_1,a_2,a_3,a_4,a_5,a_6,a_7; b_1,b_2,b_3,b_4,b_5,b_6;1]
=((a_1+1)_n(a_1-a_2-a_3+1)_n)/((a_1-a_2+1)_n(a_1-a_3+1)_n)((a_1-a_2-a_4+1)_n(a_1-a_3-a_4+1)_n)/((a_1-a_4+1)_n(a_1-a_2-a_3-a_4+1)_n),](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation28.gif) |
(30) |
where 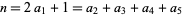 ,
, 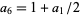 ,
, 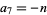 , and
, and 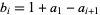 for
for 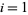 , 2, ..., 6. For all these identities,
, 2, ..., 6. For all these identities, 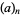 is the Pochhammer symbol.
is the Pochhammer symbol.
Gessel (1995) found a slew of new identities using Wilf-Zeilberger pairs, including the following:
![_5F_4[-a-b,n+1,n+c+1,2n-a-b+1,n+1/2(3-a-b); n-a-b-c+1,n-a-b+1,2n+2,n+1/2(1-a-b);1]=0](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation29.gif) |
(31) |
![_3F_2[-3n,2/3-c,3n+2; 3/2,1-3c;3/4]=((c+2/3)_n(1/3)_n)/((1-c)_n(4/3)_n)](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation30.gif) |
(32) |
![_3F_2[-3b,-3/2n,1/2(1-3n); -3n,2/3-b-n;4/3]=((1/3-b)_n)/((1/3+b)_n)](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation31.gif) |
(33) |
![_4F_3[3/2+1/5n,2/3,-n,2n+2; n+(11)/6,4/3,1/5n+1/2;2/(27)]=((5/2)_n((11)/6)_n)/((3/2)_n(7/2)_n)](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation32.gif) |
(34) |
(Petkovšek et al. 1996, pp. 135-137).
The following table gives various named identities ordered by the orders 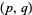 of the
of the 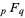 s they involve. Bailey (1935) gives a large number of such identities.
s they involve. Bailey (1935) gives a large number of such identities.
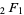 |
Gauss's hypergeometric theorem, Kummer's theorem, Orr's theorem, Ramanujan's hypergeometric identity |
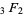 |
Darling's products, Dixon's theorem, Ramanujan's hypergeometric identity, Saalschütz's theorem, Thomae's theorem, Watson's theorem, Whipple's identity |
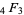 |
Clausen formula, Slater's formula, Whipple's transformation |
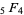 |
Dougall's theorem |
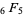 |
Whipple's identity |
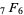 |
Dougall-Ramanujan identity, Whipple's transformation |
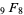 |
Bailey's transformation |
Nørlund (1955) gave the general transformation
![_nF_(n-1)[a_1,a_2,...,a_n; b_1,b_2,...,b_(n-1);xz]
=(1-z)^(-a_1)sum_(nu=0)^infty((a_1)_nu)/(nu!)_nF_(n-1)[-nu,a_2,a_3,...,a_n; b_1,b_2,...,b_(n-1);x](z/(z-1))^nu,](http://mathworld.wolfram.com/images/equations/GeneralizedHypergeometricFunction/NumberedEquation33.gif) |
(35) |
where 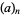 is the Pochhammer symbol. This identity is based on the transformation due to Euler
is the Pochhammer symbol. This identity is based on the transformation due to Euler
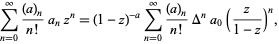 |
(36) |
where 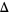 is the forward difference and
is the forward difference and
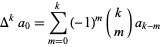 |
(37) |
(Nørlund 1955).
REFERENCES:
Bailey, W. N. "Some Identities Involving Generalized Hypergeometric Series." Proc. London Math. Soc. Ser. 2 29, 503-516, 1929.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Barnes, E. W. "The Asymptotic Expansion of Integral Functions Defined by Generalised Hypergeometric Series." Proc. London Math. Soc. 5, 59-116. 1907.
Barnes, E. W. "On Functions Defined by Simple Hypergeometric Series." Trans. Cambridge Philos. Soc. 20, 253-279, 1908a.
Barnes, E. W. "A New Development of the Theory of Hypergeometric Functions." Proc. London Math. Soc. 6, 141-177, 1908b.
Dwork, B. Generalized Hypergeometric Functions. Oxford, England: Clarendon Press, 1990.
Exton, H. Multiple Hypergeometric Functions and Applications. New York: Wiley, 1976.
Exton, H. Handbook of Hypergeometric Integrals: Theory, Applications, Tables, Computer Programs. Chichester, England: Ellis Horwood, 1978.
Gessel, I. "Finding Identities with the WZ Method." J. Symb. Comput. 20, 537-566, 1995.
Gessel, I. and Stanton, D. "Strange Evaluations of Hypergeometric Series." SIAM J. Math. Anal. 13, 295-308, 1982.
Gosper, R. W. "Decision Procedures for Indefinite Hypergeometric Summation." Proc. Nat. Acad. Sci. USA 75, 40-42, 1978.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Hypergeometric Functions." §5.5 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 204-216 1994.
Hardy, G. H. "Hypergeometric Series." Ch. 7 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 101-112, 1999.
Klein, F. Vorlesungen über die hypergeometrische Funktion. Berlin: J. Springer, 1933.
Koekoek, R. and Swarttouw, R. F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its  -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, 1-168, 1998.
Koepf, W. "Hypergeometric Database." Ch. 3 in Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, pp. 12 and 31-43, 1998.
Nørlund, N. E. "Hypergeometric Functions." Acta Math. 94, 289-349, 1955.
Petkovšek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A K Peters, 1996. http://www.cis.upenn.edu/~wilf/AeqB.html.
Rainville, E. D. Special Functions. New York: Chelsea, 1971.
Saxena, R. K. and Mathai, A. M. Generalized Hypergeometric Functions with Applications in Statistics and Physical Sciences.New York: Springer-Verlag, 1973.
Slater, L. J. Confluent Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1960.
Slater, L. J. Generalized Hypergeometric Functions. Cambridge, England: Cambridge University Press, 1966.
Zeilberger, D. "A Fast Algorithm for Proving Terminating Hypergeometric Series Identities." Discrete Math. 80, 207-211, 1990.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|