Normal Vector

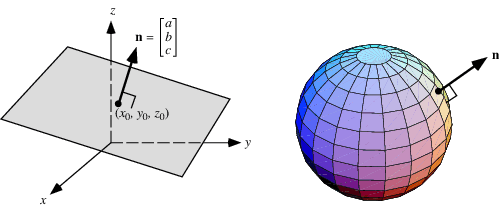
The normal vector, often simply called the "normal," to a surface is a vector which is perpendicular to the surface at a given point. When normals are considered on closed surfaces, the inward-pointing normal (pointing towards the interior of the surface) and outward-pointing normal are usually distinguished.

The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as the "unit normal." Care should be taken to not confuse the terms "vector norm" (length of vector), "normal vector" (perpendicular vector) and "normalized vector" (unit-length vector).

The normal vector is commonly denoted 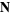 or 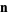, with a hat sometimes (but not always) added (i.e.,  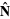and 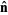) to explicitly indicate a unit normal vector.

The normal vector at a point 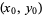 on a surface  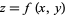is given by

(1)

where 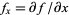 and 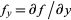 are partial derivatives.

A normal vector to a plane specified by

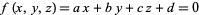(2)

is given by

(3)

where 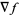 denotes the gradient. The equation of a plane with normal vector  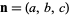passing through the point  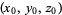is given by

(4)

For a plane curve, the unit normal vector can be defined by

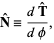(5)

where 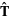 is the unit tangent vector and  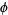is the polar angle. Given a unit tangent vector

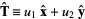(6)

with 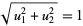, the normal is

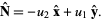(7)

For a plane curve given parametrically, the normal vector relative to the point 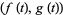 is given by

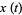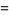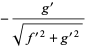			(8)
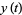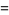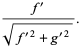			(9)

To actually place the vector normal to the curve, it must be displaced by .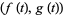

For a space curve, the unit normal is given by

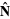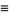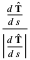			(10)
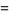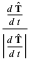			(11)
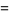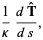			(12)

where 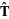 is the tangent vector,  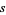is the arc length, and  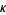is the curvature. It is also given by

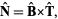(13)

where 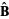 is the binormal vector (Gray 1997, p. 192).

For a surface with parametrization , the normal vector is given by

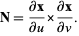(14)

Given a three-dimensional surface defined implicitly by ,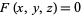

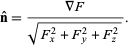(15)

If the surface is defined parametrically in the form

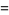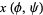			(16)
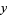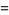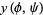			(17)
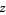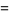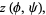			(18)

define the vectors

(19)

(20)

Then the unit normal vector is

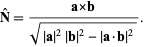(21)

Let 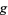 be the discriminant of the metric tensor. Then

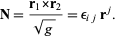(22)

REFERENCES:

Gray, A. "Tangent and Normal Lines to Plane Curves." §5.5 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 108-111, 1997.