


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 12-10-2019
Date: 30-3-2019
|
Green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Over a region 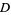 in the plane with boundary
in the plane with boundary 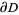 , Green's theorem states
, Green's theorem states
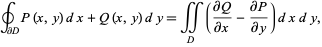 |
(1) |
where the left side is a line integral and the right side is a surface integral. This can also be written compactly in vector form as
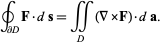 |
(2) |
If the region 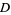 is on the left when traveling around
is on the left when traveling around 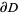 , then area of
, then area of 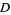 can be computed using the elegant formula
can be computed using the elegant formula
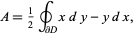 |
(3) |
giving a surprising connection between the area of a region and the line integral around its boundary. For a plane curve specified parametrically as 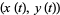 for
for ![t in [t_0,t_1]](http://mathworld.wolfram.com/images/equations/GreensTheorem/Inline7.gif) , equation (3) becomes
, equation (3) becomes
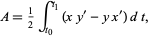 |
(4) |
which gives the signed area enclosed by the curve.
The symmetric for above corresponds to Green's theorem with 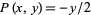 and
and 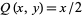 , leading to
, leading to
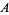 |
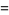 |
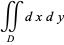 |
(5) |
 |
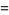 |
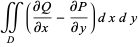 |
(6) |
 |
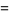 |
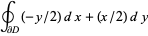 |
(7) |
 |
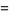 |
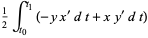 |
(8) |
 |
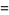 |
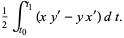 |
(9) |
However, we are also free to choose other values of 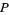 and
and 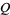 , including
, including 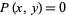 and
and  , giving the "simpler" form
, giving the "simpler" form
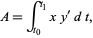 |
(10) |
and 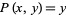 and
and 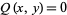 , giving
, giving
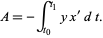 |
(11) |
A similar procedure can be applied to compute the moment about the  -axis using
-axis using 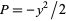 and
and 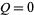 as
as
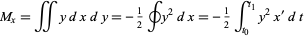 |
(12) |
and about the 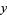 -axis using
-axis using 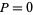 and
and 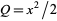 as
as
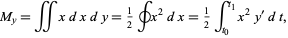 |
(13) |
where the geometric centroid 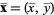 is given by
is given by 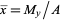 and
and 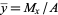 .
.
Finally, the area moments of inertia can be computed using  and
and 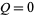 as
as
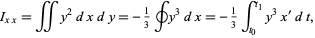 |
(14) |
using 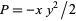 and
and 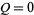 as
as
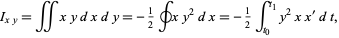 |
(15) |
and using 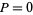 and
and 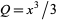 as
as
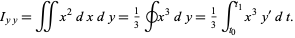 |
(16) |
REFERENCES:
Arfken, G. "Gauss's Theorem." §1.11 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 57-61, 1985.
Kaplan, W. "Green's Theorem." §5.5 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 286-291, 1991.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
عبر نقلهم بعجلات خاصة.. قسم بين الحرمين يقدم خدماته لكبار السن من الزائرين
|
|
|