Fundamental Theorems of Calculus

The first fundamental theorem of calculus states that, if 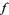 is continuous on the closed interval  and 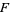 is the indefinite integral of  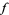on , then

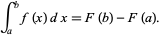(1)

This result, while taught early in elementary calculus courses, is actually a very deep result connecting the purely algebraic indefinite integral and the purely analytic (or geometric) definite integral.

The second fundamental theorem of calculus holds for 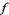 a continuous function on an open interval  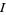and 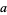 any point in 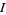, and states that if  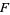is defined by

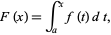(2)

then

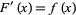(3)

at each point in .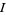

The fundamental theorem of calculus along curves states that if 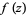 has a continuous indefinite integral  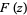in a region  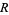containing a parameterized curve  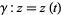for 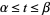, then

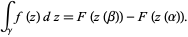REFERENCES:

Krantz, S. G. "The Fundamental Theorem of Calculus along Curves." §2.1.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 22, 1999.