المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
Theoretical background of syntax of pre- and postnominal adjectives
2025-04-12
A generalization: two positions, two classes of adjectives
2025-04-12
The specific/non-specific distinction and the position of evaluative Adjectives
2025-04-12
Degree modification on pre- and postnominal adjectives
2025-04-12
The subset property
2025-04-12
الفزياء والكون .. ميكانيكا الكم
2025-04-12

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
السيد حسين بن أبي القاسم جعفر بن حسين الموسوي
28-5-2017
هل قاعدة الكفر تشمل مطلق الكافر
2024-09-08
تبني الأيتام
21-4-2016
Leap Years
3-10-2016
المبتدأ والخبر
17-10-2014
منحنيات التعادل Neutralization curves
2023-09-18

Directional Derivative  
  
2127   01:17 مساءً   date: 15-5-2018
Author : Kaplan
Book or Source :
Page and Part : ...


Read More
Borwein Conjectures
Date: 21-8-2019 1872
Spheroidal Wave Function
Date: 25-7-2019 1986
Morgan-Voyce Polynomials
Date: 20-9-2019 1808

Directional Derivative

The directional derivative 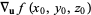del _(u)f(x_0,y_0,z_0) is the rate at which the function 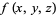f(x,y,z) changes at a point 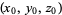(x_0,y_0,z_0) in the direction 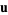u. It is a vector form of the usual derivative, and can be defined as

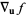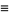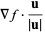del _(u)f = del f·(u)/(|u|)
(1)
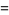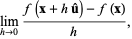= lim_(h->0)(f(x+hu^^)-f(x))/h,
(2)

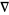where del  is called "nabla" or "del" and 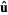u^^ denotes a unit vector.

The directional derivative is also often written in the notation

d/(ds) = s^^·del
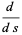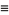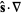(3)
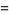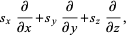= s_xpartial/(partialx)+s_ypartial/(partialy)+s_zpartial/(partialz),
(4)

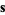where s denotes a unit vector in any given direction and 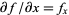partialf/partialx=f_x denotes a partial derivative.

Let 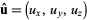u^^=(u_x,u_y,u_z) be a unit vector in Cartesian coordinates, so

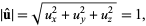|u^^|=sqrt(u_x^2+u_y^2+u_z^2)=1,
(5)

then

del _(u^^)f=(partialf)/(partialx)u_x+(partialf)/(partialy)u_y+(partialf)/(partialz)u_z.

 

 

REFERENCES:

Kaplan, W. "The Directional Derivative." §2.14 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 135-138, 1991.

Morse, P. M. and Feshbach, H. "Directional Derivatives." In Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 32-33, 1953.



الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
التاريخ / 2025-04-10

الأخبار العلمية
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
التاريخ / 2025-04-10

الساحة الاسلامية
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
التاريخ / 2025-04-12