1

المرجع الالكتروني للمعلوماتية

الرياضيات

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي

الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية

الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق

الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات

الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل

المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات

التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات

علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان

الرياضيات : الهندسة : الهندسة المستوية :

Angles-Degrees (Angles)

المؤلف:  المرجع الالكتروني للمعلوماتيه

المصدر:  www.almerja.com

الجزء والصفحة:  ...

12-3-2017

1096

 

 

We can measure Angles in Degrees.

There are 360 degrees in one Full Rotation (one 
complete circle around).

(Angles can also be measured in Radians)
 

(Note: "Degrees" can also mean Temperature, but here we are talking about Angles)

The Degree Symbol: °

We use a little circle ° following the number to mean degrees.

For example 90° means 90 degrees

One Degree


This is how large 1 Degree is

 

The Full Circle

A Full Circle is 360°

Half a circle is 180°
(called a Straight Angle)

Quarter of a circle is 90°
(called a Right Angle)

 

 

 

Why 360 degrees? Probably because old calendars (such as the Persian Calendar) used 360 days for a year - when they watched the stars they saw them revolve around the North Star one degree per day.

Also 360 can be divided evenly by 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 and 180, which makes a lot of basic geometry easier.

Measuring Degrees

We often measure degrees using a protractor:


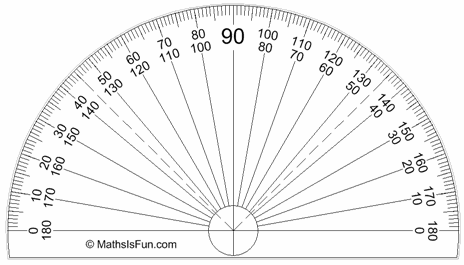
The normal protractor measures 0° to 180°

There are also full-circle protractors.

But they are not as commonly used because they are a bit big and don't do anything special.
 

Radians

 

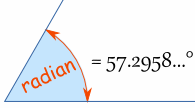
We can measure Angles in Radians.

1 Radian is about 57.2958 degrees.
 

Does 57.2958... degrees seem a strange value? 
Maybe degrees are strange, as the Radian is a pure measure based on the Radius of the circle:

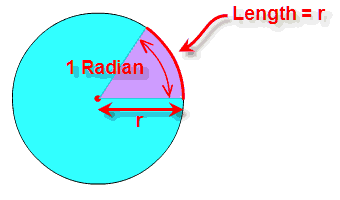
Radian: the angle made by taking the radius 
and wrapping it along the edge of a circle:

So, a Radian "cuts out" a length of a circle's circumference equal to the radius.

Radians and Degrees

So:

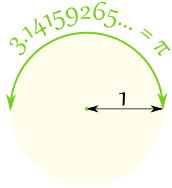
  • There are π radians in a half circle
  • And also 180° in a half circle

So π radians = 180°

So 1 radian = 180°/π = 57.2958° (approximately)

 

Degrees

Radians
(exact)

Radians
(approx)

30°

π/6

0.524

45°

π/4

0.785

60°

π/3

1.047

90°

π/2

1.571

180°

π

3.142

270°

3π/2

4.712

360°

2π

6.283
 


 

Example: How Many Radians in a Full Circle?

Imagine you cut up pieces of string exactly the length from thecenter of a circle to its edge ...

... how many pieces would you need to go around the edge of the circle?

 

Answer: 2π (or about 6.283 pieces of string). 

Radians Preferred by Mathematicians

Because the radian is based on the pure idea of "the radius being laid along the circumference", it often gives simple and natural results when used in mathematics.

For example, look at the sine function for very small values:

x (radians)

1

0.1

0.01

0.001

sin(x)

0.8414710

0.0998334

0.0099998

0.0009999998
 

 

For very small values. "x" and "sin(x)" are almost the same
(as long as "x" is in Radians!)


 

There will be other examples like that as you learn more about mathematics.

Conclusion

So, degrees are easier to use in everyday work, but radians are much better for mathematics.


Congruent Angles

Congruent Angles have the same angle (in degrees or radians). That is all.


 
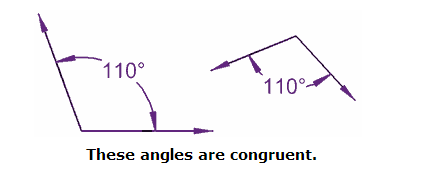
These angles are congruent.

They don't have to point in the same direction.

They don't have to be on similar sized lines.

Just the same angle.

Congruent - why such a funny word that basically means "equal"? Probably because they would only be "equal" if laid on top of each other. Anyway it comes from Latin congruere, "to agree". So the angles "agree"

Parallel Lines, and Pairs of Angles

Parallel Lines

Lines are parallel if they are always the same distance apart (called "equidistant"), and will never meet. Just remember:

Always the same distance apart and never touching.

The red line is parallel to the blue line in both these cases:

  

Example 1

  

Example 2
 


Parallel lines also point in the same direction.

 

 

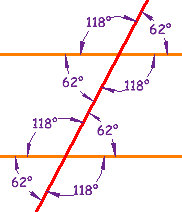
Pairs of Angles

When parallel lines get crossed by another line (which is called aTransversal), you can see that many angles are the same, as in this example:

These angles can be made into pairs of angles which have special names.

 

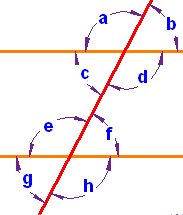
Testing for Parallel Lines

Some of those special pairs of angles can be used to test if lines really are parallel: 
 

If Any Pair Of ...

Example:

 

 

Corresponding Angles are equal, or

a = e

Alternate Interior Angles are equal, or

c = f

Alternate Exterior Angles are equal, or

b = g

Consecutive Interior Angles add up to 180°

d + f = 180°

 

 

... then the lines are Parallel

  

Examples

These lines are parallel, because a pair ofCorresponding Angles are equal.

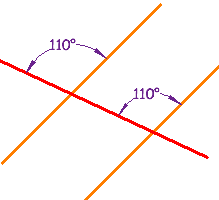
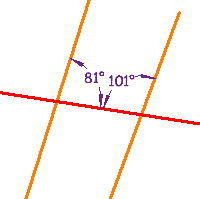
These lines are not parallel, because a pair ofConsecutive Interior Anglesdo not add up to 180° (81° + 101° =182°)

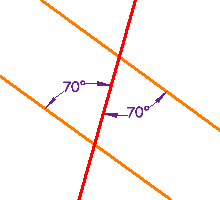
These lines are parallel, because a pair of Alternate Interior Angles are equal

 

 


Transversals

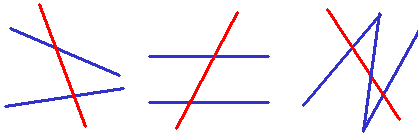
A Transversal is a line that crosses at least two other lines.



The red line is the transversal in each example:
 

Transversal crossing two lines

this Transversal crosses twoparallel lines

... and this one cuts across three lines
 

 


Triangles Contain 180°

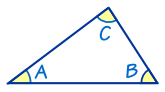
In a triangle, the three angles always add to 180°:

A + B + C = 180°
 

Try it yourself (drag the points):

We can use that fact to find a missing angle in a triangle:

Example: Find the Missing Angle "C"

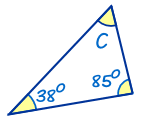
Start With:

 

A + B + C = 180°

 

 

 

Fill in what we know:

 

38° + 85° + C = 180°

 

 

 

Rearrange

 

C = 180° - 38° - 85°

 

 

 

Calculate:

 

C = 57°
 

Proof

This is a proof that the angles in a triangle equal 180°:

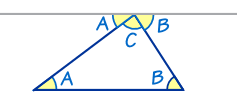
The top line (that touches the top of the triangle) is 
running parallel to the base of the triangle.

So:

  • angles A are the same
  • angles B are the same

And you can easily see that A + C + B does a complete rotation from one side of the straight line to the other, or 180°

 

Supplementary Angles

Two Angles are Supplementary if they add up to 180 degrees.


 

These two angles (140° and 40°) are Supplementary Angles, because they add up to 180°.

Notice that together they make astraight angle.

 

 

But the angles don't have to be together.

These two are supplementary because 60° + 120° = 180°

 

 

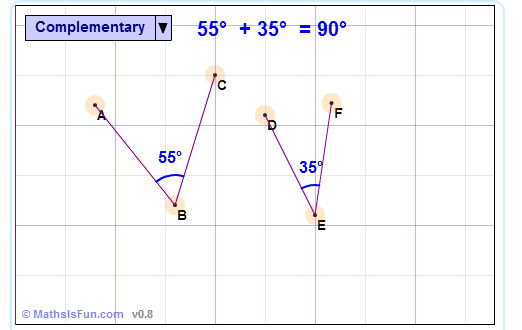
Complementary Angles

Two angles are Complementary when they 
add up to 90 degrees (a Right Angle ).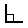

 

These two angles (40° and 50°) are
Complementary Angles, because they add up to 90°.

Notice that together they make a right angle .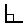

 

 

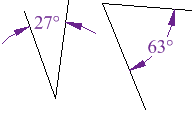
But the angles don't have to be together.

These two are complementary because 27° + 63° = 90°

 


 

Right Angled Triangle

In a right angled triangle, the two non-right angles are complementary, because in a triangle the three angles add to 180°, and 90° has already been taken by the right angle.

 

 

EN

تصفح الموقع بالشكل العمودي