MO theory: heteronuclear diatomic molecules

In this section, we return to MO theory and apply it to hetero nuclear diatomic molecules. In each of the orbital interaction diagrams constructed for homonuclear diatomics, the resultant MOs contained equal contributions from each atomic orbital involved. This is represented in equation below for the bonding MO in H₂ by the fact that each of the wavefunctions ψ₁ and ψ₂ contributes equally to MO, and the representations of the MOs in H₂ depict symmetrical orbitals. Now we look at representative examples of diatomics in which the MOs may contain different atomic orbital contributions, a scenario that is typical for heteronuclear diatomics.    (1.1)

First, we must consider likely restrictions when we are faced with the possibility of combining different types of atomic orbitals. Which orbital interactions should be considered?. We stated that orbital interactions are allowed if the symmetries of the atomic orbitals are compatible with one another. In our approach to the bonding in a diatomic, we made the assumption that only the interactions between like atomic orbitals, e.g. 2s–2s, 2pz–2pz, need be considered. Such interactions are symmetryallowed, and in addition, in a homonuclear diatomic the energies of like atomic orbitals on the two atoms are exactly matched.

In a heteronuclear diatomic, we often encounter two atoms that have different basis sets of atomic orbitals, or have sets of similar atomic orbitals lying at different energies. For example, in CO, although both C and O possess valence 2s and 2p atomic orbitals, the greater effective nuclear charge of O means that its atomic orbitals lie at a lower energy than those of C. Before we look more closely at some examples of heteronuclear diatomics, let us briefly consider some symmetry-allowed and disallowed orbital interactions. It is important to remember that we are looking at these symmetry properties with respect to the internuclear axis. In our earlier discussion of homonuclear diatomics, we ignored the possibility of overlap between the px and py orbitals. Such an interaction between orthogonal p atomic orbitals (Figure 1.1a) would give a zero overlap integral. Similarly, for nuclei lying on the z axis, interaction between px and pz, or py and pz, orbitals gives zero overlap. An interaction between an s and a p atomic orbital may occur depending upon the orientation of the p orbital. In Figure 1.1b, overlap would be partly bonding and partly antibonding and the net effect is a non-bonding interaction. On the other hand, Figure 1.1 c shows an s–p interaction that is allowed by symmetry.

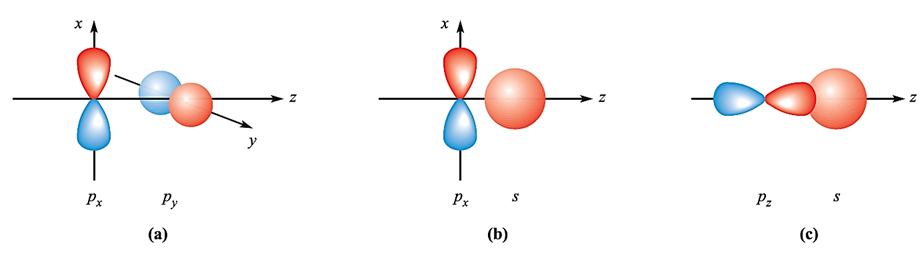
Fig. 1.1 Overlap between atomic orbitals is not always allowed by symmetry. Combinations (a) and (b) lead to non-bonding situations but (c) is symmetry-allowed and gives rise to a bonding interaction.

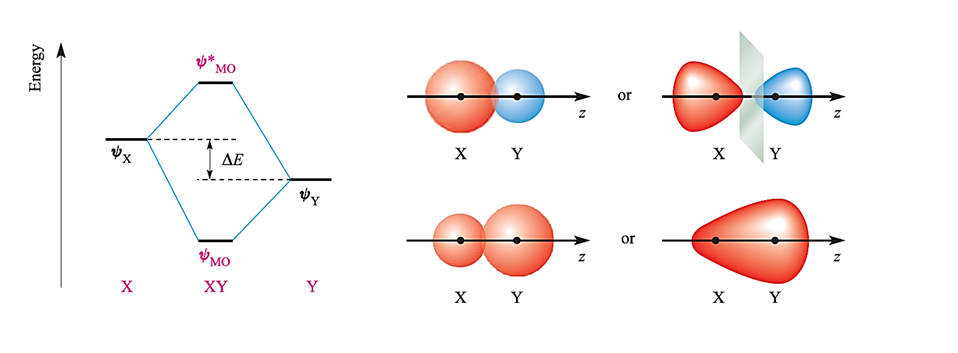
Fig. 1.2 The relative energies of atomic orbitals of X and Y will dictate whether an interaction (formally allowed by symmetry) will lead to efficient overlap or not. Here, an interaction occurs but the contribution made by Y to ψMO is greater than that made by ψX, while ψX contributes more than ψY to the antibonding MO. The diagrams on the right give pictorial representations of the bonding and antibonding MOs.

Whether or not this leads to effective overlap depends upon the relative energies of the two atomic orbitals. This is illustrated in Figure 1.2 for a diatomic XY. Let the interaction between ψ_X and ψ_Y be symmetry-allowed; the orbital energies are not the same but are close enough that overlap between the orbitals is efficient. The orbital interaction diagram shows that the energy of the bonding MO is closer to E(ψ_Y) than to E)ψ_X( and the consequence of this is that the bonding orbital possesses greater Y than X character. This is expressed in equation 1.2 in which c₂ > c₁. For the antibonding MO, the situation is reversed, and ψ_X contributes more than ψ_Y; in equation 1.3, c₃ > c₄.

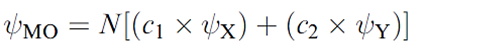
(1.2)

                (1.3)

The energy separation ΔE in Figure 1.2 is critical. If it is large, interaction between ψ_X and ψ_Y will be inefficient (the overlap integral is very small). In the extreme case, there is  no interaction at all and both ψ_X and ψ_Y appear in the XY molecule as unperturbed non-bonding atomic orbitals. We illustrate this below.

Hydrogen fluoride

The ground state configurations of H and F are 1s  and [He]2s² 2p⁵ respectively. Since Z_eff(F) ˃Z_eff(H), the F 2s and 2p atomic orbital energies are significantly lowered with respect to the H 1s atomic orbital (Figure 1.3). We now have to consider which atomic orbital interactions aresymmetry-allowed and then ask whether the atomic orbitals are sufficiently well energy-matched. First, define the axis set for the orbitals; let the nuclei lie on the z axis. Overlap between the H 1s and F 2s orbitals is allowed by symmetry, but the energy separation is very large (note the break on the energy axis in Figure 1.3).

Overlap between the H 1s and F 2p_z atomic orbitals is also symmetry-allowed and there is a reasonable orbital energy match. As Figure 1.3 shows, an interaction occurs leading to σ and σ* MOs; the σ-orbital has greater F than H character. Notice that, because HF is non-centrosymmetric the symmetry labels of the orbitals for HF do not involve g and u labels. The two F 2p_x and 2py atomic orbitals become non-bonding orbitals in HF since no net bonding interaction with the H 1s atomic orbital is possible. Once the orbital interaction diagram has been constructed, the eight valence electrons are accommodated as shown in Figure 1.3, giving a bond order of 1 in HF. The MO picture of HF indicates that the electron density is greater around the F than H nucleus; the model is consistent with a polar H^__F bond in the sense H^δ+__F^δ-. [Exercise: Sketch pictorial representations of the σ  and σ*  MOs in HF. Hint: Refer to Figure 1.2.]

Fig. 1.3 An orbital interaction diagram for the formation of HF. Only the valence atomic orbitals and electrons are shown. The break in the vertical (energy) axis indicates that the energy of the F 2s atomic orbital is much lower than is actually shown.

مواضيع ذات صلة

Ligand field theory

Crystal field theory

Limitations of VSEPR theory

 Molecular shape and the VSEPR model Valence-shell electron-pair repulsion theory

The octet rule

The bonding in He2, Li2 and Be2

Molecular orbital theory applied to the bonding in H2

 Homonuclear diatomic molecules: molecular orbital (MO) theory

The valence bond (VB) model applied to F2, O2 and N2

The valence bond (VB) model of bonding in H2

Covalent bond distance, covalent radius and van der Waals radius

Bonding models: an introduction