A multiple use of runoff elections was discussed by Marie Jean Antoine Nicolas Caritat, Marquis de Condorcet, an eighteenth Century French mathematician and political theorist. (Similar ideas were proposed by Ramon Llull as long ago as 1299.)

Suppose we simultaneously conduct all the “runoff” elections among our candidates. For example, in the election discussed in Sample Problem 1.2in(Preferential Voting: The Hare Method), there are six runoffs: A versus B, A versus C, A versus D, B versus C, B versus D, and C versus D. If any one candidate wins all his/her runoffs, then surely you would consider that person a winner. We shall call such a candidate a Condorcet winner.

In Sample Problem 1.1in(Sequential Voting), we find:

                       B beats A 10–9,

                      A beats C 16–3,

                      B beats C 12–7,

so B is a Condorcet winner. Similarly, in Sample Problem 1.2in(Preferential Voting: The Hare Method),, D is a Condorcet winner. But even in the simple example

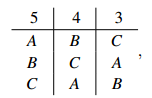
A beats B 8 – 4, B beatsC 9 – 3 andC beats A 7 – 5, so there is no Condorcet winner.

In elections with several candidates, it is very common to have no Condorcet winner, even when there are no ties. This is a serious fault in the Condorcet method.

Condorcet’s own solution to this problem is as follows. We shall construct an ordered list of the candidates. Look at all the runoffs and find out which candidate won with the biggest majority. Looking at Sample Problem 1.1in(Sequential Voting), again, the biggest majority was A beat C 16–3. We’ll denote this A → C. Then look for the secondbiggest,  then the third-biggest, and so on, and make a list:

A → C(16−3),B → C(12−7),B → A(10−9).

Now go through this list and construct a preference order of the candidates. At each step, if X → Y, then X precedes Y in the preference list, unless Y already precedes X in the list. In our example, we must have A before C, B before C and B before A.

The list is BAC and clearly B is the winner.

We shall refer to this solution as Condorcet’s extended method, to distinguish it from the case where there is a Condorcet winner under the original method. Note that, if there is a Condorcet winner, the same candidate also wins under the extended method.

Let us apply this to the above example

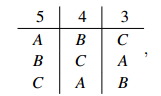
which has no Condorcet winner. We have, with the larger majorities preceding smaller ones,

B → C(9−3),A → B(8−4),C → A(7−5).

From B → C and A → B we get the list ABC. Next we see C → A, but A already precedes C, so this result is ignored. The final list is ABC, and A is elected, even though a majority of voters would prefer C to A.

Sample Problem 1.1 Consider the election with preference profile:

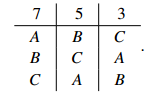
Who would win under the Hare method? Is there a Condorcet winner? Who wins under Condorcet’s solution method?

Solution. The votes for A, B and C are 7, 5 and 3 respectively. Under the Hare method, C is eliminated. The new preference profile is:

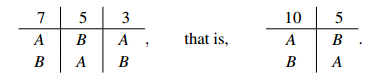
So A wins 10 – 5. Looking at all three runoffs, we see that A beats B 10 – 5,  B beats C 12 – 3 and C beats A 8 – 7, so there is no Condorcet winner. For Condorcet’s solution, we see

B → C(12−3),A → B(10−5),C → A(7−5).

مواضيع ذات صلة

Remez Algorithm

Quadratic Phase Array

Fractional Fourier Transform

Circulant Matrix

Logistic Map--r=-2

Logistic Map--r=2

Logistic Map--r=4

Lotka-Volterra Equations

Population Growth

Survivorship Curve

Tent Map

Traveling Salesman Problem