
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Werner Heisenberg
المؤلف:
William H. Cropper
المصدر:
Great Physicists
الجزء والصفحة:
11-12-2015
4266
Werner Heisenberg

Twins
The birth of the grand synthesis of quantum theory now known as “quantum mechanics” was not the happy event it might have been. To everyone's surprise, what came into the world was not one infant but two twins. And to make matters worse, the two births were months apart, with different doctors officiating; there were even some ugly rumors about the parentage of the two arrivals. Erwin Schrodinger and his colleagues in Munich and Berlin, who claimed the child they called “wave mechanics,” found little to admire in the other child, called “matrix mechanics,” claimed by Werner Heisenberg and his friends in Gottingen and Copenhagen. Said Schrodinger about matrix mechanics: “I was discouraged, if not repelled, by what seemed to me a rather difficult method of transcendental algebra, defying any visualization.” And Heisenberg had this to say about wave mechanics in a letter to Wolfgang Pauli: “The more I think about the physical portion of the Schrodinger theory, the more repulsive I find it. . . . What Schrodinger writes about visualizability ‘is probably not quite right’ [one of Bohr's favorite euphemisms], in other words it's crap.” For a time, it appeared that physics would have to support two infant versions of quantum mechanics, with an embarrassing rivalry on matters of heritage and title. But fortunately there were some who appreciated and understood both children. All were relieved to find that both twins were healthy and legitimate and deserving of the family name, quantum mechanics.
A New Mechanics
Heisenberg made his breakthrough at almost the same time that Pauli developed his exclusion principle. Recall that in Pauli's view the atomic landscape could be seen ultimately as a fine-grained system of stationary states occupied by electrons according to the dictates of the exclusion principle. Pauli's theory was a major step in the evolution of the concept of quantization. Planck had introduced energy quanta; Einstein had built a theory of radiation quanta or photons; and Bohr had constructed a picture of atoms existing in quantized stationary states. Pauli began to unify these theoretical fragments by enumerating the stationary states with quantum numbers.
However, Pauli's work was itself fragmentary as a theoretical edifice because the fourfold set of quantum numbers he postulated was based as much on empirical knowledge as on theoretical derivation. There was an urgent need for a general theory that deduced the quantum numbers rather than postulating them. Physicists still searched for a grand synthesis that encompassed the entire quantum realm, starting with a few mathematical statements. Heisenberg took the first confident steps on this theoretical path. He put together the beginnings of a theory that eventually probed deeply into the dynamic workings of atoms. It was an atomic mechanics constructed in parallel to Newton's mechanics, but the resemblance was formal and abstract. Heisenberg shaped his theory with what Leon Rosenfeld called “formal virtuosity.” Like Einstein,
Heisenberg found his creative principle in mathematics. He once remarked that “it was natural for me to use a formal mathematical view which in some respects was an esthetic judgment.”
By simplifying the axiomatic beginnings, and by building along mathematical lines, Heisenberg avoided the pitfalls distressing Bohr's theory. Without committing himself concerning the physical status of individual atomic electrons, he managed to build a dynamics that resembled the mathematical form of Newtonian mechanics and its elaborations. In an efficient, abstract way, he bridged the ordinary world and the atomic world. Bohr had crossed this bridge earlier, but with the difference that he had visualized the inner workings of atoms with some of the attributes of large-scale objects, such as the orbital motion of planets. Heisenberg's bridge to the atomic realm was formal and thoroughly mathematical, and it offered no such convenient images of atomic interiors.
Heisenberg was building in a style of theoretical architecture that was unfamiliar in atomic physics. This was an approach guided by mathematical models that formally resembled the Newtonian equations of motion, but was otherwise based only vaguely, if at all, on classical models or “pictures.” The essential attitude, which soon became and remained dominant in quantum theory, was later bluntly summarized by Paul Dirac: “The main object of physical science is not the provision of pictures, but is the formulation of laws governing phenomena and the applications of these laws to the discovery of new phenomena. If a picture exists, so much the better; but whether a picture exists or not is a matter of only secondary importance.”
Heisenberg's analysis worked with two fundamental physical ingredients, both of which were simple and observable, although neither helped much in the framing of physical pictures. First was the set of frequencies emitted by an atom when it jumps between stationary states in the manner originally proposed by Bohr. If an atom performs one of these quantum jumps downward from the higher energy E2 to the lower energy E1, a spectral “line” is emitted whose frequency, call it v21, is specified by the Bohr rule,
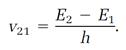
This concept is generalized to specify any frequency vmn emitted when an atom jumps between any two stationary states whose energies are Em and En,

The entire set of frequencies {vmn} collects all the lines observable in the atom's emission spectrum.
The second basic ingredient in Heisenberg's analysis evolved from a problem implied but not solved in Bohr's theory. Bohr had used the concept of atoms jumping between stationary states, but he could not cope with the problem of how one knew when and where a particular atom was going to make a particular kind of jump. This was a difficulty Rutherford had immediately spotted when he saw Bohr's first papers. “It seems to me,” he wrote to Bohr in 1913, “that you would have to assume that the electron [about to jump] knows beforehand where it is going to stop.” Rutherford was asking for a deterministic mechanism like those familiar in classical physics.
Bohr never managed to make his theory work that way, but he later took a valuable hint from a paper written by Einstein in 1916. The idea had occurred to Einstein that atoms making quantum jumps are like disintegrating radioactive atoms. Predictions concerning the when and where of individual radioactive disintegrations had also proved impossible, and in the absence of a better procedure, the laws of radioactivity had for some time been formulated statistically, as predictions of what probably would happen to a radioactive atom. From the viewpoint of an individual atom, this is an indeterminate description because the statistical statement says nothing with certainty about individual processes; it is an account of average behavior inferred from data taken on a very large number of atoms. Einstein saw that this statistical description could be extended to all atomic change. Among other things, he managed “in an amazingly simple and general way” to arrive at Planck's radiation law by defining probabilities for the occurrence of all possible atomic transitions. Bohr took up this theme and found a place in his own atomic theory for Einstein's “transition probabilities.”
So we find Heisenberg in 1925 extending the Einstein-Bohr canon. The second physical constituent in Heisenberg's analytical recipe, accompanying the set of spectral frequencies {vmn}, was a set of transition probabilities. If the probability for the m-to-n transition, labeled let's say Amn, is large, the transition is likely to occur, and the spectral line whose frequency is vmn is intense. Thus the transition probabilities are theoretical manifestations of the observable spectral line intensities.
Heisenberg found that the transition probabilities Amn and the frequencies vmn could be used in a method of calculation that resembled a well-established technique known as “Fourier analysis” (invented by Joseph Fourier in the early nineteenth century for his analytical theory of heat). For each observable quantity known in Newtonian mechanics, Heisenberg found a quantum counterpart that was recognizable as a “Fourier expansion,” formulated with the frequencies and the transition probabilities.
In later developments, the sets of transition probabilities were arranged in square arrays with all the entries concerning state 1 in row 1, entries for state 2 in row 2, and so forth. If a total of three states is involved, the square array has the appearance
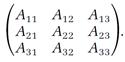
Guided by the Fourier procedure, which was mostly a mathematical technique, and striving for a dynamics that formally resembled Newtonian mechanics when the arrays were replaced by corresponding classical variables, Heisenberg arrived at a workable quantum mechanics.
Matrix Mechanics
“Heisenberg's latest paper, soon to be published, appears rather mystifying but is certainly true and profound,” Born wrote to Einstein in July 1925. To Born, it was clear that a genuine quantum mechanics was at hand, and he began developing a full mathematical statement of the theory. He was particularly intrigued by the remarkable multiplication rule: “Heisenberg's symbolic multiplication rule did not give me rest, and after days of concentrated thinking and testing I recalled an algebraic theory I had learned from my teacher, Rosanes, in Breslau.” The algebraic theory concerned “matrices,” mathematical arraylike entities, whose algebra had been formulated by Arthur Cayley, with a mathematician's foresight, some seventy years earlier. The peculiar multiplication rule discovered by Heisenberg was strictly analogous to matrix multiplication; the Heisenberg arrays were formally identifiable as matrices. Once Born had this clue, the way was cleared for the development of a quantum “matrix mechanics.” That work was started by Born, Heisenberg, and a young matrix expert, Pascual Jordan.
Born and Heisenberg found themselves in an alien mathematical world in which they were not fluent with the language. “I do not even know what a matrix is,” Heisenberg complained to Jordan. As it happened, however, the Gottingen physicists were not lacking in good advice on how to handle their mathematical difficulties. The great mathematician David Hilbert also lived in Gottingen, and he, better than anyone in the world, spoke the mathematical language the physicists needed to learn. Edward Condon, an American who was on the Gottingen scene, tells about Hilbert’s advice: “Hilbert was having a great laugh on Born and Heisenberg and the Gottingen theoretical physicists because when they first discovered matrix mechanics they were having, of course, the same kind of trouble that everybody else had in trying to solve problems and to manipulate and really do things with matrices. So they went to Hilbert for help.”
Hilbert told them that for him matrices were handy devices for bringing out certain formal aspects of problems written in another mathematical idiom, that of differential equations. Because physicists had for many years exploited the language of differential equations to great advantage in other problems, Hilbert suggested that the matrices might be manifestations of more-useful equations of the differential kind. According to Condon, the Gottingen theorists thought that was “a goofy idea and that Hilbert did not know what he was talking about.” But Hilbert was rarely wrong. Just six months later, Erwin Schrodinger found the equations Hilbert had prophesied, and demonstrated that they accomplished the same things as matrix mechanics and more with the familiar methods of differential equations.
 الاكثر قراءة في علماء الفيزياء
الاكثر قراءة في علماء الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















