Spectroscopic terms
المؤلف:
Peter Atkins, Tina Overton, Jonathan Rourke, Mark Weller, and Fraser Armstrong
المصدر:
Shriver and Atkins Inorganic Chemistry ,5th E
الجزء والصفحة:
ص489-490
2025-09-28
400
Spectroscopic terms
Key points: Different microstates exist for the same electronic configuration; for light atoms, Russell Saunders coupling is used to describe the terms, which are specified by symbols in which the value of L is indicated by one of the letters S, P, D,..., and the value of 2S+1 is given as a left superscript.
we expressed the electronic structures of atoms by giving their electronic con figurations, the designation of the number of electrons in each orbital (as in 1s22s1 for Li). However, a configuration is an incomplete description of the arrangement of electrons in atoms. In the configuration 2p2, for instance, the two electrons might occupy orbitals with different orientations of their orbital angular momenta (that is, with different values of ml from among the possibilities +1, 0, and 1 that are available when l=1). Similarly, the designation 2p2 tells us nothing about the spin orientations of the two electrons ms=+1/ 2 or -1/2. The atom may in fact have several different states of total orbital and spin angular momenta, each one corresponding to the occupation of orbitals with different values of ml by electrons with different values of Ms.
The different ways in which the electrons can occupy the orbitals specified in the configuration are called the microstates of the con figuration. For example, one microstate of a 2p2 configuration is (1+ ,1- ); this notation signifies that both electrons occupy an orbital with ml=1 but do so with opposite spins, the superscript indicating ms 1 2 and indicating ms1. Another microstate of the same configuration is (-1 ,+0 ). In this microstate, both electrons have ms=1/2 one occupies the 2p orbital with ml=-1 and the other occupies the orbital with ml=0.
The microstates of a given configuration have the same energy only if electron-electron repulsions on the atom are negligible. However, because atoms and most molecules are compact, interelectronic repulsions are strong and cannot always be ignored. As a result, microstates that correspond to different relative spatial distributions of electrons have different energies. If we group together the microstates that have the same energy when electron-electron repulsions are taken into account, we obtain the spectroscopically distinguishable energy levels called terms.
For light atoms and the 3d series, it turns out that the most important property of a micro state for helping us to decide its energy is the relative orientation of the spins of the electrons.
Next in importance is the relative orientation of the orbital angular momenta of the electrons. It follows that we can identify the terms of light atoms and put them in order of energy by sorting the microstates according to their total spin quantum number S (which is determined by the relative orientation of the individual spins) and then according to their total orbital angular momentum quantum number L (which is determined by the relative orientation of the individual orbital angular momenta of the electrons). For heavy atoms, such as those of the 4d and 5d series, the relative orientations of orbital momenta or of spin momenta are less important. In these atoms the spin and orbital angular momenta of individual electrons are strongly coupled together by spin orbit coupling, so the relative orientation of the spin and orbital angular momenta of each electron is the most important feature for determining the energy. The terms of heavy atoms are therefore sorted on the basis of the values of the total angular momentum quantum number j for an electron in each microstate.
The process of combining electron angular momenta by summing first the spins, then the orbital momenta, and finally combining the two resultants is called Russell Saunders coupling. This coupling scheme is used to identify the terms of light atoms (i.e. the 3d metals), and we consider it in detail here. The coupling scheme most appropriate to heavy atoms (that is, atoms of the 4d and 5d series of elements) is called jj-coupling, but we shall not consider it further.
Our first task is to identify the values of L and S that can arise from the orbital and spin angular momenta of individual electrons. Suppose we have two electrons with quantum numbers l1 , s1 and l2 , s2 . Then, according to the Clebsch Gordan series, the possible values of L and S are
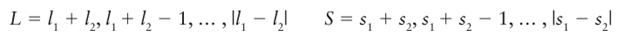
(Themodulus signs appear because neither L nor S can, by definition, be negative.) For example, an atom with configuration d2 (l1=2, l2=2) can have the following values of L:
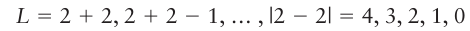
The total spin (because s1=1/2 , s2=1/2 ) can be
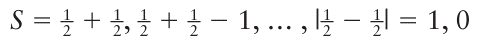
To find the values of L and S for atoms with three electrons, we continue the process by combining l3 with the value of L just obtained, and likewise for s3. Once L and S have been found, we can write down the allowed values of the quantum numbers ML and MS,
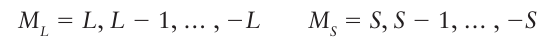
These quantum numbers give the orientation of the angular momentum relative to an arbitrary axis: there are 2L+1 values of ML for a given value of L and 2S+1 values of MS for a given value of S. The values of ML and MS for a given microstate can be found very easily by adding together the values of ml or ms for the individual electrons. Therefore, if one electron has the quantum number ml1 and the other has ml2 , then ML=ml1+ml2
A similar expression applies to the total spin: MS=ms1+ms2
Thus, for example, (0+,-1-) is a microstate with ML=0-1=-1 and MS=1/2 +(-1/2) =0 and may contribute to any term for which these two quantum numbers apply. By analogy with the notation s, p, d, … for orbitals with l 0, 1, 2,…, the total orbital angular momentum of an atomic term is denoted by the equivalent uppercase letter:
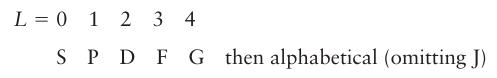
The total spin is normally reported as the value of 2S+1, which is called the multiplicity of the term:
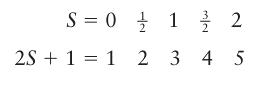
The multiplicity is written as a left superscript on the letter representing the value of L, and the entire label of a term is called a term symbol. Thus, the term symbol 3P denotes a term (a collection of nearly degenerate states) with L=1and S=1, and is called a triplet term.
الاكثر قراءة في مواضيع عامة في الكيمياء العضوية
اخر الاخبار
اخبار العتبة العباسية المقدسة
