Jackson,s Difference Fan
المؤلف:
Conway, J. H. and Guy, R. K.
المصدر:
"Jackson Difference Fans." In The Book of Numbers. New York: Springer-Verlag
الجزء والصفحة:
pp. 84-85
28-11-2021
1262
Jackson's Difference Fan
If, after constructing a difference table, no clear pattern emerges, turn the paper through an angle of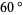 
and compute a new table. If necessary, repeat the process. Each rotation reduces powers by 1, so the sequence ![<span style=]()
{k^n}" src="https://mathworld.wolfram.com/images/equations/JacksonsDifferenceFan/Inline2.gif" style="height:15px; width:23px" /> multiplied by any polynomial in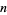 
is reduced to 0s by a 
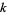-fold difference fan.
Call Jackson's difference fan sequence transform the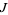 
-transform, and define 
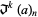as the 
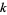-th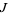 
-transform of the sequence ![<span style=]()
{a_i}_(i=0)^n" src="https://mathworld.wolfram.com/images/equations/JacksonsDifferenceFan/Inline9.gif" style="height:17px; width:38px" />, where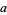 
and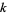 
are complex numbers. This is denoted
When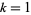 
, this is known as the binomial transform of the sequence. Greater values of 
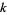give greater depths of this fanning process.
The inverse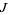 
-transform of the sequence ![<span style=]()
{b_i}_(i=0)^n" src="https://mathworld.wolfram.com/images/equations/JacksonsDifferenceFan/Inline15.gif" style="height:17px; width:38px" /> is given by
When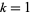 
, this gives the inverse binomial transform of ![<span style=]()
{b_i}_(i=0)^n" src="https://mathworld.wolfram.com/images/equations/JacksonsDifferenceFan/Inline17.gif" style="height:17px; width:38px" />.
REFERENCES:
Conway, J. H. and Guy, R. K. "Jackson's Difference Fans." In The Book of Numbers. New York: Springer-Verlag, pp. 84-85, 1996.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
