Surreal numbers are the most natural collection of numbers which includes both the real numbers and the infinite ordinal numbers of Georg Cantor. They were invented by John H. Conway in 1969. Every real number is surrounded by surreals, which are closer to it than any real number. Knuth (1974) describes the surreal numbers in a work of fiction.

The surreal numbers are written using the notation {a|b}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline1.gif" style="height:18px; width:33px" />, where {|}=0" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline2.gif" style="height:18px; width:43px" />, {0|}=1" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline3.gif" style="height:18px; width:47px" /> is the simplest number greater than 0, {1|}=2" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline4.gif" style="height:18px; width:47px" /> is the simplest number greater than 1, etc. Similarly, {|0}=-1" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline5.gif" style="height:18px; width:60px" /> is the simplest number less than 0, etc. However, 2 can also be represented by {1|3}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline6.gif" style="height:18px; width:33px" />, {3/2|4}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline7.gif" style="height:18px; width:48px" />, {1|omega}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline8.gif" style="height:18px; width:39px" />, etc.

Some simple games have abbreviated names that can be expressed in terms of surreal numbers. 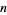For example, {0|0}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline9.gif" style="height:18px; width:62px" />, {0|}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline10.gif" style="height:18px; width:47px" />, {n-1|}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline11.gif" style="height:18px; width:69px" /> for an integer , {0|1}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline13.gif" style="height:18px; width:72px" />, {0|*}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline14.gif" style="height:18px; width:63px" />, and {*|0}" src="https://mathworld.wolfram.com/images/equations/SurrealNumber/Inline15.gif" style="height:18px; width:65px" />. Most surreal numbers can be represented as hackenbush positions.

REFERENCES:

Berlekamp, E. R.; Conway, J. H.; and Guy, R. K. Winning Ways for Your Mathematical Plays, Vol. 1: Games in General. London: Academic Press, 1982.

Conway, J. H. On Numbers and Games. New York: Academic Press, 1976.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 283-284, 1996.

Conway, J. H. and Jackson, A. "Budding Mathematician Wins Westinghouse Competition." Not. Amer. Math. Soc. 43, 776-779, 1996.

Gonshor, H. An Introduction to Surreal Numbers. Cambridge, England: Cambridge University Press, 1986.

Knuth, D. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. Reading, MA: Addison-Wesley, 1974. http://www-cs-faculty.stanford.edu/~knuth/sn.html.

Schleicher, D. and Stoll, M. "An Introduction to Conway's Numbers and Games." http://arxiv.org/abs/math.CO/0410026.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.