The Menger sponge is a fractal which is the three-dimensional analog of the Sierpiński carpet.

The 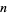th iteration of the Menger sponge is implemented in the Wolfram Language as MengerMesh[n, 3].

Let 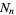 be the number of filled boxes,  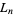the length of a side of a hole, and  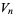the fractional volume after the th iteration, then

			(1)
			(2)
			(3)

The capacity dimension is therefore

			(4)
			(5)
			(6)
			(7)

(OEIS A102447).

The Menger sponge, in addition to being a fractal, is also a super-object for all compact one-dimensional objects, i.e., the topological equivalent of all one-dimensional objects can be found in a Menger sponge (Peitgen et al. 1992).

The image above shows a metal print of the Menger sponge created by digital sculptor Bathsheba Grossman (http://www.bathsheba.com/).

REFERENCES:

 Dickau, R. "Sierpinski-Menger Sponge Code and Graphic." http://library.wolfram.com/infocenter/MathSource/4662/.

Dickau, R. M. "Menger (Sierpinski) Sponge." http://mathforum.org/advanced/robertd/sponge.html.

Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 101, 1988.

Grossman, B. "Menger Sponge." http://www.bathsheba.com/math/menger.

Kosmulski, M. "Modulus Origami--Fractals, IFS." http://hektor.umcs.lublin.pl/~mikosmul/origami/fractals.html.

Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 145, 1983.

Mosely, J. "Menger's Sponge (Depth 3)." http://world.std.com/~j9/sponge/.

Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992.

Sloane, N. J. A. Sequence A102447 in "The On-Line Encyclopedia of Integer Sequences."

Werbeck, S. "A Journey into Menger's Sponge." http://www.angelfire.com/art2/stw/.