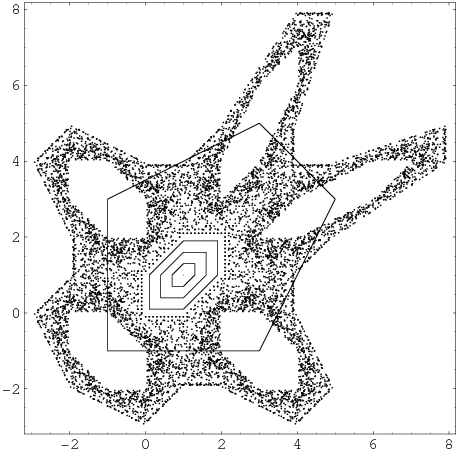
A two-dimensional piecewise linear map defined by

			(1)
			(2)

The map is chaotic in the filled region above and stable in the six hexagonal regions. Each point in the interior hexagon defined by the vertices (0, 0), (1, 0), (2, 1), (2, 2), (1, 2), and (0, 1) has an orbit with period six (except the point (1, 1), which has period 1). Orbits in the other five hexagonal regions circulate from one to the other. There is a unique orbit of period five, with all others having period 30. The points having orbits of period five are (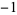, 3), (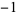, 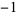), (3, 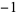), (5, 3), and (3, 5), indicated in the above figure by the black line. However, there are infinitely many distinct periodic orbits which have an arbitrarily long period.

REFERENCES:

Devaney, R. L. "A Piecewise Linear Model for the Zones of Instability of an Area Preserving Map." Physica D 10, 387-393, 1984.

Devaney, R. L. "The Gingerbreadman." Algorithm 3, 15-16, Jan. 1992.

Dr. Mu. "Cowculations: Gingerbread Man." Quantum, pp. 55-57, January/February 1998.

Peitgen, H.-O. and Saupe, D. (Eds.). "A Chaotic Gingerbreadman." §3.2.3 in The Science of Fractal Images. New York: Springer-Verlag, pp. 149-150, 1988.