الصياغة الرياضية لمبدأ التراكب

لقد حدث تغير عميق خلال القرن الحالي (الماضي) في آراء الفيزيائيين التي اعتنقوها عن الأسس الرياضية لموضوعهم. لقد افترضوا سابقًا أن مبادئ ميكانيكا نيوتن تقدم الأساس لوصف كل الظواهر الفيزيائية وأن ما على الفيزيائي النظري عمله هو أن يطور ويطبق هذه المبادئ. مع الاعتراف بأنه لا يوجد سبب منطقي يجعل مبادئ نيوتن والمبادئ التقليدية صالحة خارج نطاق تحقيقها تجريبيٍّا، وأصبح إدراك التخلي عن الأفكار التقليدية ضرورة واجبة. هذا التخلي تم التعبير عنه من خلال تقديم صياغة رياضية جديدة ومجموعة بديهيات جديدة وقواعد للمعالجة أدخلت إلى طرق الفيزياء النظرية. تزودنا ميكانيكا الكم بمثال جيد للأفكار الجديدة حيث وجب ربط حالات منظومة ديناميكية بالمتغيرات الديناميكية بطرق غريبة تمامًا تستعصي على الفهم من وجهة النظر التقليدية. ويتطلب تمثيل الحالات والمتغيرات الديناميكية كميات رياضية ذات طبيعة مختلفة عما هو مستخدم عادة في الفيزياء. والمشروع الجديد يصبح نظرية فيزيائية دقيقة عندما تكون كل البديهيات والقواعد العملية التي تحكم الكميات الرياضية محددة، بالإضافة إلى طرح قوانين معينة تربط الحقائق الفيزيائية بالصياغة الرياضية بحيث إنه يمكن استخلاص معادلات بين شروط فيزيائية معطاة وكميات رياضية، والعكس بالعكس، وفي أي تطبيق للنظرية يمكن للمرء أن يعطي معلومات فيزيائية معينة ويود أن يشرع في التعبير عنها بواسطة معادلات بين كميات رياضية.

وعندئذ يود المرء استنتاج معادلات جديدة بمساعدة البديهيات والقواعد العملية ثم يود أن يختم بتفسير هذه المعادلات الجديدة كشروط فيزيائية. تعتمد تزكية المشروع، بعيدًا عن التوافق الداخلي، على اتفاق النتائج النهائية مع التجربة.

سوف نبدأ ببناء المشروع بمعالجة العلاقات الرياضية بين حالات منظومة ديناميكية عند لحظة زمنية. وهذه العلاقات سوف تأتي من الصيغة الرياضية لمبدأ التراكب. وعملية التراكب هي نوع من عمليات الإضافة وتؤدي إلى أنه يمكن إضافة الحالات بطريقة ما لتنتج حالات جديدة. وبناء على ذلك يجب أن ترتبط الحالات بكميات رياضية من النوع الذي يمكن جمع عدد منها ليعطي كميات أخرى من نفس النوع. وأوضح أمثلة لهذه الكميات هي المتجهات. والمتجهات المعتادة الموجودة في فراغ في أبعاد محدودة ليست كافية عمومًا لمعظم المنظومات الديناميكية في ميكانيكا الكم. ويجب علينا أن نلجأ إلى التعميم لمتجهات في فراغ ذي أبعاد لانهائية، وتتعقد المعالجة الرياضية بظهور أمثلة لمسألة التقارب. وحاليٍّا سوف نتناول فقط بعض خواص المتجهات العامة وهي الخواص التي يمكن استنتاجها على أساس مشروع بسيط من البديهيات، بينما لا نتعرض لمسائل التقارب والموضوعات المرتبطة بها حتى تظهر الحاجة لذلك.

من المستحسن أن يكون لدينا اسمًا خاصٍّا لوصف المتجهات التي ترتبط بحالات منظومة ما في ميكانيكا الكم، سواء كانت هذه المتجهات في فراغ عدد أبعاده محدود أو لانهائي الأبعاد سوف نسميها بمتجهات Ket *. او ببساطة كيتات Kets (المتجهات اليمنى) ونعبر عن متجه عام لواحد منها برمز خاص ⟩|. وإذا أردنا أن نميز واحدًا منها بعلامة A مثلا نضعه في المنتصف ⟩A|.

وسوف تتضح مناسبة هذا الترميز عند تطوير المشروع ويمكن أن يُضرب متجه أيمن (Ket) في عدد مركب ويمكن ان تجمع المتجهات اليمنى (kets) مع بعضها لتعطي متجهات يمنى اخرى. فمثلا من المتجهين الأيمنين Ket |B⟩, A⟩| يمكننا ان نكون

​

حيث c₁, c₂ عددان مركبان. ويمكن أيضاً ان نجري على المتجهات اليمنى عمليات خطية عامة مثل اضافة عدد لا نهائي منها. واذا كان لدينا متجه أيمن|x⟩ معتمدا على بارامتر x يمكن أن يأخذ كل القيم في مدى معين فيمكن أن نجري التكامل بالنسبة للبارامتر x وللحصول على متجه أيمن (Ket) آخر هو :

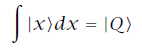
المتجه الأيمن والمعبر عنه خطيٍّا بدلالة متجهات يمنى أخرى معينة يقال إنه معتمد عليها. وتسمى فئة المتجهات مستقلة خطيٍّا إذا لم يكن من الممكن التعبير خطيٍّا عن أي واحد منها بدلالة باقي الفئة. والآن نفترض أن كل حالة لمنظومة ديناميكية عند لحظة معينة تناظر متجهًا أيمن، والتناظر يكون بحيث إذا نتجت حالة من تراكب حالات أخرى معينة يكون المتجه الأيمن المناظر لها معبرًا عنه خطيٍّا بدلالة المتجهات اليمنى للحالات الأخرى وبالعكس. وهكذا فإن الحالة R تنتج من تراكب الحالتين A,B عندما تكون المتجهات اليمنى المناظرة مرتبطة بالمعادلة (1).

يؤدي الافتراض السابق إلى خواص معينة لعملية التراكب، تلك الخواص في الحقيقة ضرورية لتكون كلمة « تراكب » ملائمةً. وعندما تتراكب حالتان أو أكثر فالترتيب في  عملية التراكب ليس مهمٍّا، ولذا فإن عملية التراكب تكون متماثلة بين الحالات المتراكبة. ومرة أخرى من معادلة (1) انه (باستثناء الحالة عندما يتلاشى اي من c₁ او c₂) يمكن تكوين الحالة R بتراكب حالتي A,B، ومن ثم فان الحالة A يمكن ان تتكون من تراكب ,B,R وكذلك يمكن تكوين B من تراكب A,R. وعلاقة التراكب تكون متماثلة بين الحالات الثلاث A,B,R.

يقال للحالة التي تنتج من تراكب حالات أخرى معينة إنها معتمدة على هذه الحالات. ولمزيد من التعميم سيقال إن حالة ما معتمدة على فئة من الحالات محدودة أو لانهائية العدد إذا كان المتجه الأيمن المناظر لهذه الحالة معتمدًا على المتجهات اليمنى المناظرة لفئة الحالات، ويقال لمجموعة الحالات إنها مستقلة إذا لم تكن أي حالة منها معتمدة على باقي الحالات.

وحتى نستطيع أن نتقدم بالصيغ الرياضية لمبدأ التراكب يجب أن نتزود بافتراض إضافي وهو أنه بتراكب حالة ما مع نفسها فلا يمكن أن نحصل على حالة جديدة ولكن نسترجع الحالة الأصلية مرة أخري. فإذا كانت الحالة الأصلية تناظر متجهًا أيمن   |A⟩ فعندما تتراكب مع نفسها فالحالة الناتجة سوف تناظر

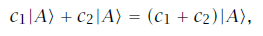
حيث c₁, c₂   أعداد. والآن قد يكون لدينا c₁ + c₂ = 0 وفي هذه الحالة تكون نتيجة عملية التراكب لا شيء. فقد لاشت المركبات بعضها البعض بتأثير التداخل. ويستدعي افتراضنا الجديد أنه بعيدًا عن هذه الحالة الخاصة، فإن الحالة الناتجة يجب أن تكون نفس الحالة الأصلية وبحيث إن (c₁ +c₂)|A⟩ يجب ان تناظر الحالة نفسها A⟩| والآن c₁ + c₂ ما هو الا ما هو إلا عدد مركب اختياري، ومن ثم يمكننا استنتاج أنه إذا ضرب المتجه الأيمن المناظر لحالة ما في أي عدد مركب غير مساوي للصفر، فإن المتجه الناتج يناظر الحالة نفسها (الحالة الأصلية). ومن ثم فإن أي حالة تتميز باتجاه المتجه الأيمن بينما أي طول يحدده المرء للمتجه الأيمن يكون غير ذي أهمية. وكل حالات المنظومة الديناميكية تكون في تناظر واحد لواحد مع كل الاتجاهات الممكنة للمتجهات اليمنى ولا يمكن التفريق بين اتجاهي المتجهين اليمينين A⟩| او A⟩|-.

يُظهر الافتراض الذي سبق ذكره بوضوح جلي الاختلاف الأساسي بين التراكب في نظرية الكم وأي نوع من التراكب الكلاسيكي. وفي حالة المنظومات الكلاسيكية التي يستقيم فيها مبدأ التراكب فعندما يتم تراكب حالة ما مع نفسها، بالنسبة لغشاء متذبذب مثلًا، فإن النتيجة هي حالة مختلفة بسعات ذبذبات مختلفة. ليس هناك خصائص فيزيائية مميزة تتميز كيفيٍّا، للحالة الكمية المناظرة لقيم الترددات الكلاسيكية الموصوفة بنسب السعات عند نقط مختلفة من الغشاء. مرة أخرى نكرر، بينما توجد حالة كلاسيكية بسعة ذبذبات مساوية للصفر في كل مكان، هي حالة السكون؛ فإنه لا توجد حالة مناظرة لهذه المنظومة الكمية، حيث إن المتجه الأيمن الصفري لا يناظر أي حالة على الإطلاق.

إذا أعطينا حالتين مناظرتين لمتجهين أيمنين ⟩, |B⟩|Aوالحالة العامة المتولدة من تراكبهما تناظر متجهًا أيمن |R⟩ والذي يتحدد بعددين مركبين هما العاملين   c₁, c₂ في معادلة (1)، إذا ضرب هذان العاملان في عامل واحد )هو نفسه عدد مركب) فإن المتجه الايمن⟩ |Rسوف يضرب في هذا العامل بينما لا تتغير الحالة المناظرة. ولذا فإن النسبة بين هذين العاملين هي المؤثرة في تحديد الحالة R . وعليه فإن الحالة تعرف بعدد مركب واحد أو ببارامترين حقيقيين. وبذلك فمن حالتين معطاتين يمكن الحصول على عدد لانهائي من الدرجة الثانية من الحالات من خلال التراكب. أي يمكن الحصول على عدد لانهائي ثنائي الطيات )two-fold infinity²∞) من الحالات عن طريق التراكب.

 (*) يلاحظ ان Ket هي المقطع الاخير من كلمة BRACKET التي تعني (قوسا) وسيتخذ المقطع الأول للمرافق كما سيتضح فيما بعد، ويرمز للقوس بالرمز ⟨⟩ وعليه أخذت ⟩|لتمثلKet ،|⟨ لتمثل bta. وستعتمد فيما يلي كلمة (متجه أيمن)، لتعبر عن Ket و(متجه أيسر) لتعبر عن bta.