Visualization and comparison with a ‘Newtonian’ star

From the continuous matching of the grr-component we can derive the relation 1 − 2m/R_ּ = 1 − R²_ּ/ ˆR². Together with the definition of the Schwarzschild radius we find for the total gravitating mass of the star

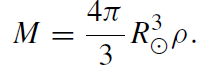 (1.1)

Another method for obtaining the total mass is to multiply the density ρ by the spatial volume of the star at a given time t₀. However, the total mass calculated that way is larger than the total gravitating mass (1.1). This is due to the fact that not mass (that is ‘rest mass’) alone but mass-energy gravitates. The negative gravitational binding forces thus contribute to the gravitating mass which appears in the metric.

Finally, some words about the geometry of the Schwarzschild spacetime. We can visualize its structure by means of an embedding in the following way: In the equatorial plane ϑ = π/2 at a prescribed time t = t₀, the metric reads ( ˆR ² = R³_ּ /2m):

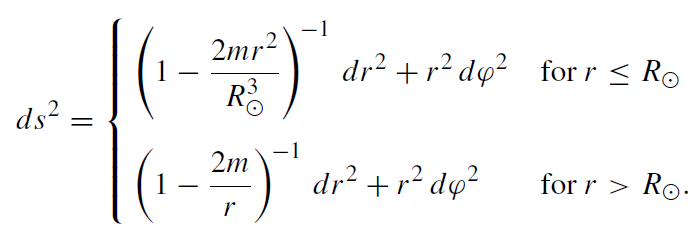 (1.2)

These metrics are equivalent to 2D metrics induced by the 3D Euclidean metric on a sphere or a hyperboloid, respectively. The 3D Euclidean metric is ds² = dr² + r ² dφ² + dz². A surface rotationally symmetric around the z-axis is described by a parametrization z = z(r ). The metric induced on this surface is ds² = [1+(dz/dr)²] dr² +r ² dφ². By comparison with the previous metrics, we extract differential equations for z(r ) which can be easily solved. At r = R_ּ, the surfaces are continuously joined (see figure 1.1).

Outside, we have the usual vacuum Schwarzschild geometry which was discussed extensively in the previous section. We may add a few remarks. Obviously, a circle (or sphere, respectively) around the origin has a circumference of 2πr, where r is the radial Schwarzschild coordinate. We also observe that the proper distance measured by a freely falling observer (who, in our picture, moves radially on the hyperboloid) is larger than the coordinate distance Δr . Inside the star we have the three-geometry of a sphere with radius ˆR. Far away from the star we find flat Euclidean geometry.

The structure of this three-geometry resembles the Newtonian case. Inside, we have a conformally flat space, where the Weyl (‘trace-free part of the curvature’) vanishes and the Ricci tensor is proportional to the mass-energy density. In the Newtonian case, the trace of the tidal matrix (the analogy to curvature) is proportional to the mass density, and, subsequently, its trace-free part vanishes. Outside, in vacuum, it is the other way around. There the trace parts are zero (K_aa = 0 and Ric_αβ = 0 = R). The Newtonian tidal acceleration

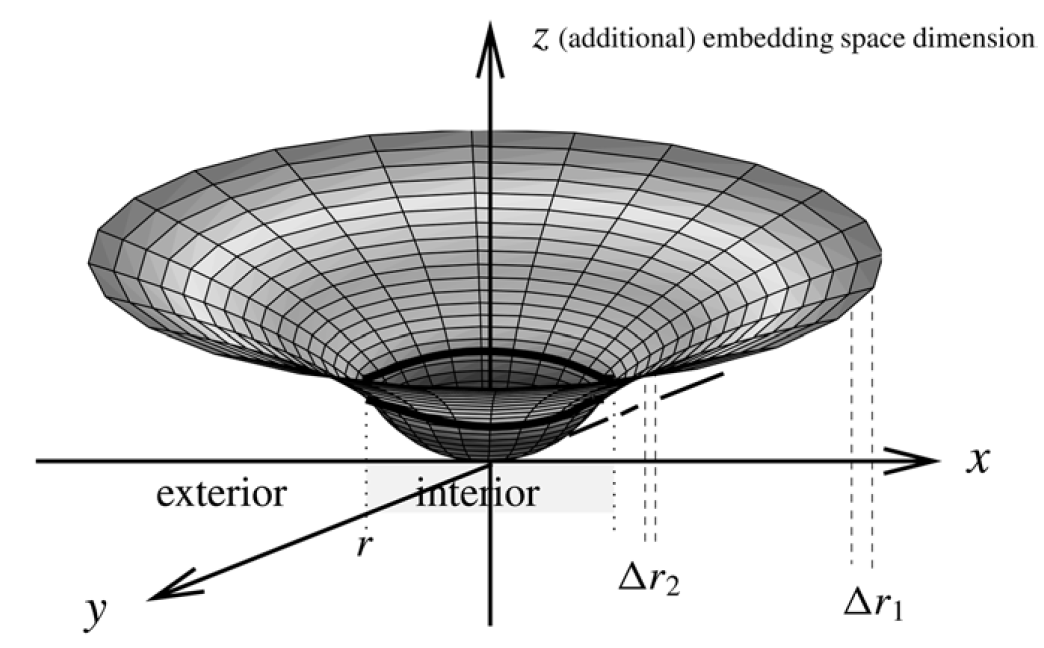
Figure 1.1. Geometry of Schwarzschild spacetime.

matrix is trace free and reads (in Cartesian coordinates, assume r = (0, 0, r )):

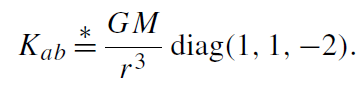 (1.3)

In Einstein's theory we have to use the equation for the geodesic  in order to calculate the relative acceleration of two freely falling test particles. For the comoving observer, with u^α = (c, 0, 0, 0) and in an orthonormal frame, we find

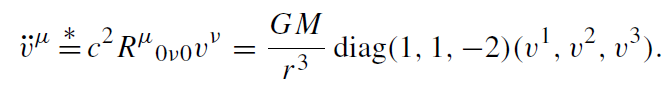 (1.4)

Thus, in a special frame, we have the same tidal accelerations as in the Newtonian case.

Accordingly, the gravitational field of a spherically symmetric body in Newton's 3D theory is very naturally embedded into Einstein's 4D theory.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

ثورة النسبية المكان والزمان في أزمة

التأثير في الزمن: ثبات سرعة الضوء وتهاوي المفهوم المطلق للزمن

أبعاد أكثر مما تراه العين

النسبية العامة في مواجهة ميكانيكا الكم

المكان والزمان وعين الراصد

هل هي موجة أم جسيمة؟

الحاجة إلى نظرية جديدة النسبية العامة في مواجهة ميكانيكا الكم

(التأثير في الزمن) تأثير الحركة على مرور الزمن: الساعة الضوئية وتباطؤ الزمن

الحركة خلال الزمكان (Spacetime)

تموجات في نسيج الزمكان: حين لحقت الجاذبية بالضوء (حل التناقض)

مرة أخرى اعوجاج الزمان(حين يتباطأ الزمن تحت ثقل الجاذبية)

التسارع واعوجاج المكان والزمان