Flat Minkowski spacetime, null coordinates, and the Penrose diagram

In this section, we are going to analyze the Schwarzschild solution, in particular its singularity structure. For this purpose we will first have a look at null coordinates. The simplest testing ground in this context is the (flat) Minkowski space. Its metric, in Cartesian and spherical polar coordinates, reads (c = 1) as

 ds² = −dt² + dx² + dy² + dz² = −dt² + dr² + r ² dΩ².   (1.1)

We define advanced and retarded null coordinates as follows

v := t +r      u:= t − r (1.2)

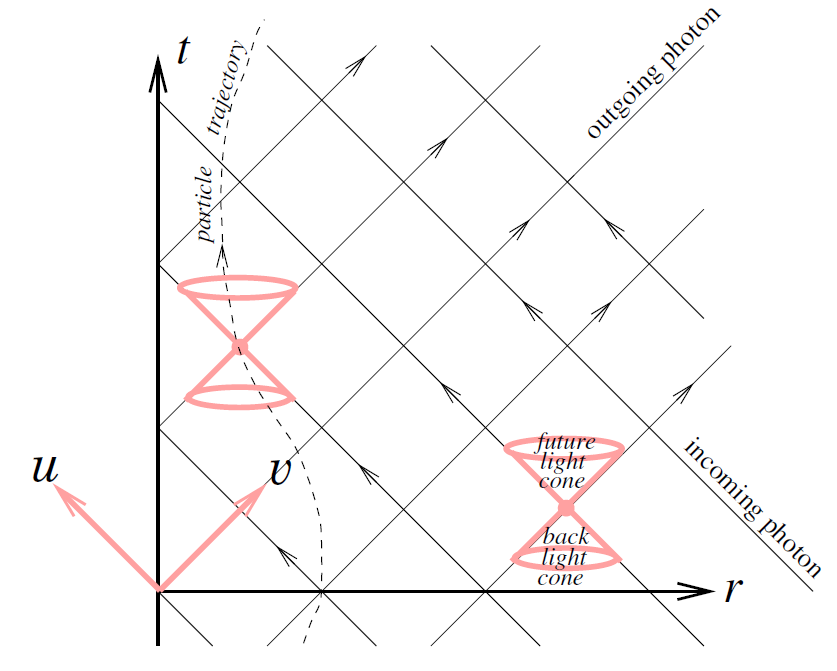
Figure 1.1. Minkowski spacetime in null coordinates.

and find that

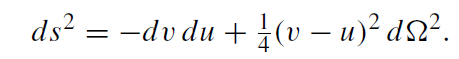 (1.3)

In figure 1.1 we show the Minkowski spacetime in terms of the new coordinates. Incoming photons, i.e. pointlike particles with velocity ˙ r = −c = −1, move on paths with v = constant. Correspondingly, we have for outgoing photons u = constant. The special relativistic wave equation is solved by any function f (u) and f (v). The surfaces f (u) = constant and f (v) = constant represent the wavefronts which evolve with the velocity of light. The trajectory of every material particle with v < c = 1 has to remain inside the region defined by the surface r = t. In an (r, t)-diagram this surface is represented by a cone, the so called light cone. Any point in the future light cone r = t can be reached by a particle or signal with a velocity less than c. A given spacetime point P can be reached by a particle or signal from the spacetime region enclosed by the back light cone r = −t.

We can map, following Penrose, the infinitely distant points of spacetime into finite regions by means of a conformal transformation which leaves the light cones intact. Then we can display the whole infinite Minkowski spacetime on a (finite) piece of paper. Accordingly, introduce the new coordinates

 (1.4)

Then the metric reads as

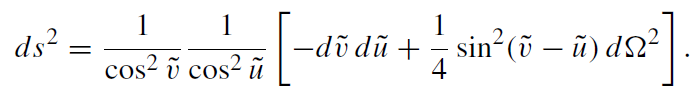 (1.5)

We can go back to time- and spacelike coordinates by means of the transformation

 (1.6)

see (1.1). Then the metric reads as

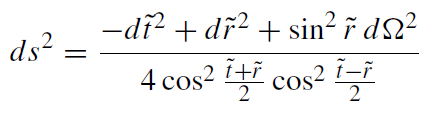 (1.7)

that is, up to the function in the denominator, it appears as a flat metric. Such a metric is called conformally flat (it is conformal to a static Einstein cosmos). The back-transformation to our good old Minkowski coordinates reads:

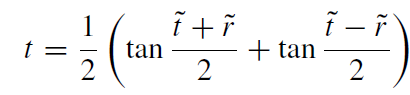           (1.8)

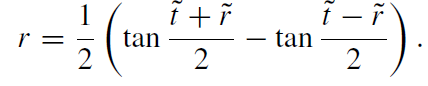 (1.9)

Our new coordinates ˜t , ř extend only over a finite range of values, as can be seen from (1.8), (1.9). Thus, in the Penrose diagram of a Minkowski spacetime, we can depict the whole Minkowski spacetime, with a coordinate singularity along ř = 0. All trajectories of uniformly moving particles (with velocity smaller than c) emerge from one single point, past infinity I ⁻, and all will eventually arrive at the one single point I⁺, namely at future infinity. All incoming photons have their origin on the segment ⁻ (script I ⁻ or ‘scri minus’), lightlike past infinity, and will run into the coordinate singularity on the ˜t-axis. All outgoing photons arise from the coordinate singularity and cease on the line ⁺, lightlike future infinity (‘scri plus’). The entire spacelike infinity is mapped into the single point I ⁰.

Now, we have a really compact picture of the Minkowski space. Next, we would like to proceed along similar lines in order to obtain an analogy for the Schwarzschild spacetime.