Space Station Pressure

A space station consists of a large cylinder of radius R₀ filled with air. The cylinder spins about its symmetry axis at an angular speed Ω providing an acceleration at the rim equal to g. If the temperature τ is constant inside the station, what is the ratio of air pressure P_c at the center of the station to the pressure P₀ at the rim?

SOLUTION

The rotation of the station around its axis is equivalent to the appearance of an energy U = -mΩ²R²/2, where m is the mass of an air particle and R is the distance from the center. Therefore, the particle number density satisfies the Boltzmann distribution (similar to the Boltzmann distribution in a gravitational field):

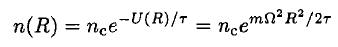
Where n_c is the number density at the center and τ ≡ k_BT is the temperature in energy units. The pressure is related to the number density n simply by P = nτ. So, at constant temperature,

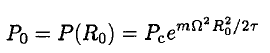
Using the condition that the acceleration at the rim is Ω²R₀ = g, we have