


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-8-2016
Date: 1-8-2016
Date: 16-3-2021
|
Quantum Corrections to Equation of State
Consider a noninteracting, one-component quantum gas at temperature τ, with a chemical potential μ in a cubic volume V. Treat the separate cases of bosons and fermions.
a) For a dilute system derive the equation of state in terms of temperature τ, pressure P, particle density n, and particle mass m. Do this derivation approximately by keeping the leading and next-leading powers of n. Interpret your results as an effective classical system.
b) At a given temperature, for which densities are your results valid?
SOLUTION
a) Start with the particle distribution over the absolute value of momentum:
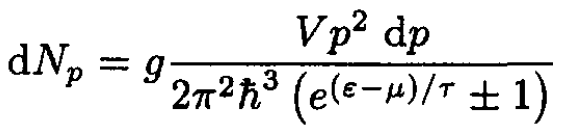 (1)
(1)
where the upper sign in (S.4.68.1) and below corresponds to Fermi statistics and the lower to Bose (g = 2s + 1). Using ε = p2/2m, we obtain
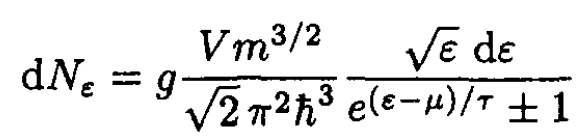 (2)
(2)
The total energy is given by
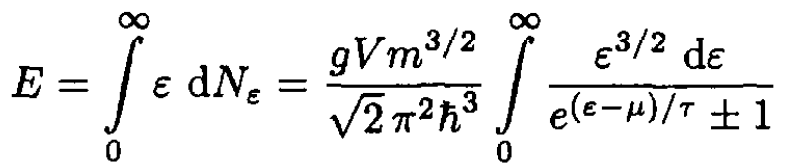 (3)
(3)
On the other hand, using the grand canonical potential Ω, where
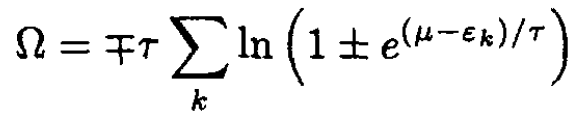 (4)
(4)
and replacing the sum by an integral, using (2), we obtain
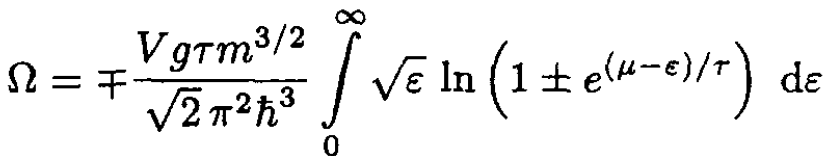 (5)
(5)
Integrating (5) by parts, we have
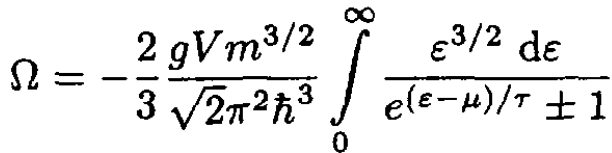 (6)
(6)
Comparing this expression with (3), we find that
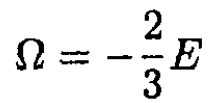 (7)
(7)
However, Ω = F – μN = F – G = -PV. Therefore, we obtain the equation of state, which is valid both for Fermi and Bose gases (and is, of course, also true for a classical Boltzmann gas):
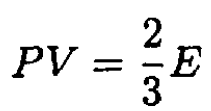 (8)
(8)
Note that (8) was derived under the assumption of a particular dispersion law ε = p2/2m; for relativistic particles or photons with ε = pc, (8) becomes PV = E/3. From (8) and (3), we obtain
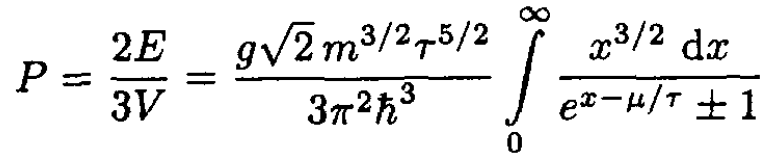 (9)
(9)
where x ≡ ε/τ. (9) defines the equation of state. To find quantum corrections to the classical equation of state (which corresponds to the case eμ/τ << 1), expand the integral in (9), using exp (μ/τ – x) as a small parameter:
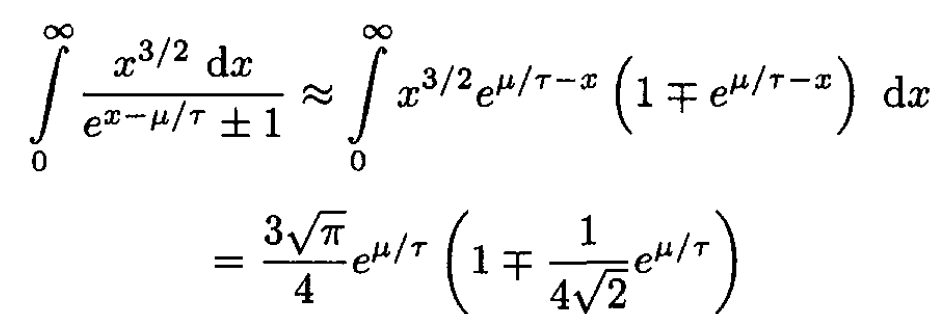 (10)
(10)
Using Ω = -PV and substituting (10) into (9), we have
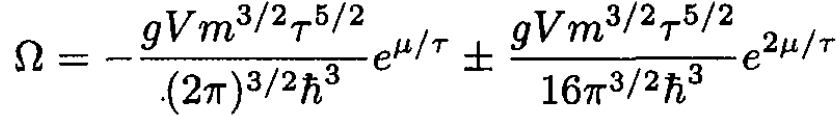 (11)
(11)
The first term, which we may call ΩB, corresponds to a Boltzmann gas with g = 1, and the second term gives the first correction
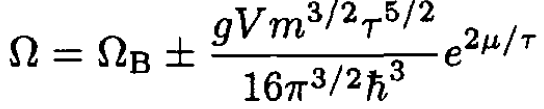 (12)
(12)
Using the fact that, for small corrections
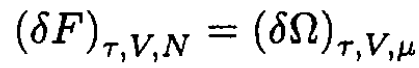
we can write the first quantum correction to the free energy F. Using the classical expression for μ in terms of τ and V gives the result to the same accuracy:
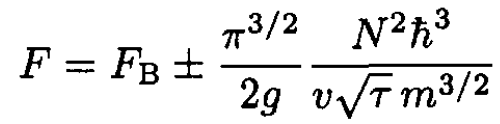 (13)
(13)
Using
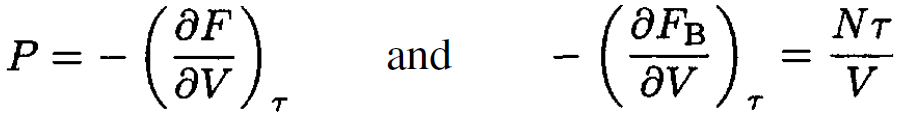
we obtain, from (13),
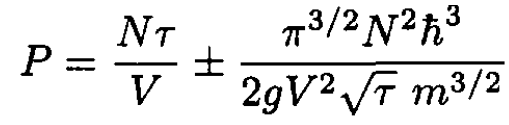 (14)
(14)
and
 (15)
(15)
where n ≡ N/V.
b) The condition for validity of this approximation is that the first correction should be much less than unity:
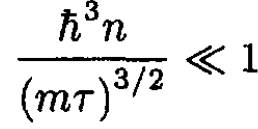 (16)
(16)
This gives the condition on the density for which (15) is valid:
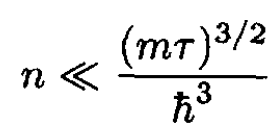 (17)
(17)
It is interesting to determine the de Broglie wavelength λdB at this temperature τ. We find that
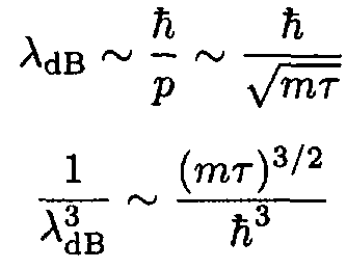
We see that this approximation is valid when the separation between particles is much larger than the de Broglie wavelength. (16) expresses the same condition as for the applicability of Boltzmann statistics (which implies exp (μ/τ) << 1). Since the chemical potential μ may be written
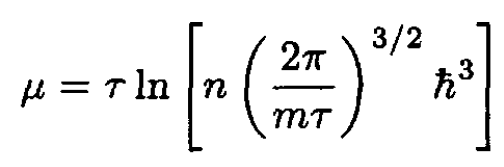 (18)
(18)
we see that
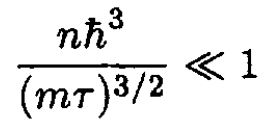



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
طالبات جامعة واسط: بارتدائنا العباءة نبيّن بأنّ إرث السيدة الزهراء (عليها السلام) ممتد للأجيال
|
|
|