Three Masses and Three Springs on Hoop

Three masses, each of mass m are interconnected by identical massless springs of spring constant k and are placed on a smooth circular hoop as

Figure 1.1

shown in Figure 1.1. The hoop is fixed in space. Neglect gravity and friction. Determine the natural frequencies of the system, and the shape of the associated modes of vibration.

SOLUTION

Introducing x_i, the displacement from equilibrium for respective masses 1,2,3 (see Figure 1.2), we can write a Lagrangian in the form

Figure 1.2

The resulting equations of motion are in the form

(1)

Again, looking for solutions of the form x_i = A_i e^iωt, we obtain an equation for the determinant:

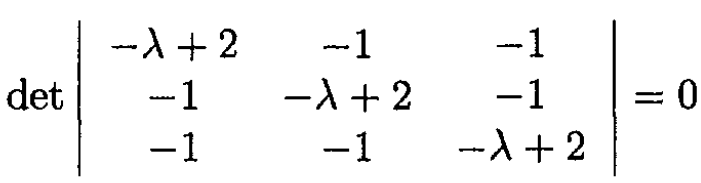
Where λ = ω²/ω²₀ and ω²₀ = k/m. The first root is λ₁ = ω = 0 which corresponds to the movement of all three masses with the same velocity. The two other roots are 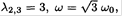 which are double degenerate, corresponding to the mode A₁ = 3, A₂ = -A₃, or A₂ = 0, A₁ = -A₃, where one mass is at rest and the two others move in opposite directions. The result can be obtained even without solving (1), if one can guess that this is the mode. Then

So, again,