
Square Well
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 56
الجزء والصفحة:
part 2 , p 56
 22-8-2016
22-8-2016
 1752
1752
Square Well
A particle of mass m is confined to a space 0 < x < a in one dimension by infinitely high walls at x = 0, a. At t = 0 the particle is initially in the left half of the well with constant probability
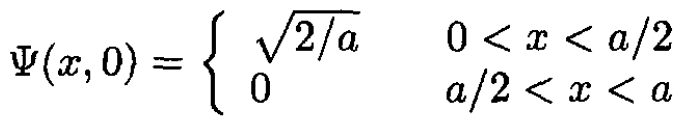 (i)
(i)
a) Find the time-dependent wave function ψ (x, t).
b) What is the probability that the particle is in the nth eigenstate?
c) Write an expression for the average value of the particle energy.
SOLUTION
a) The most general solution is
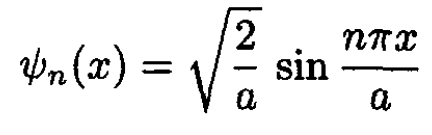 (1)
(1)
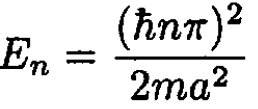 (2)
(2)
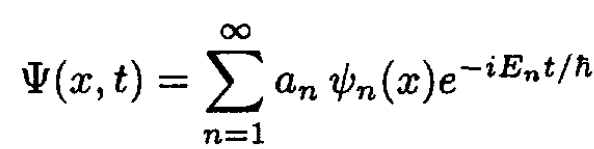 (3)
(3)
We evaluate the coefficients by using the initial condition at t = 0:
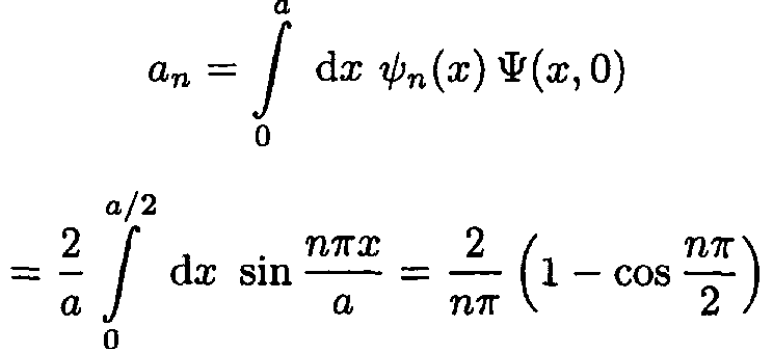 (4)
(4)
The term cos (nπ/2) is either 1, 0, or –1, depending on the value of n. The answer to (a) is to use the above expression for an in (S.5.11.3). The answer to part (b) is that the probability of being in the nth eigenstate is |an|2. The answer to part (c) is that the average value of the energy is
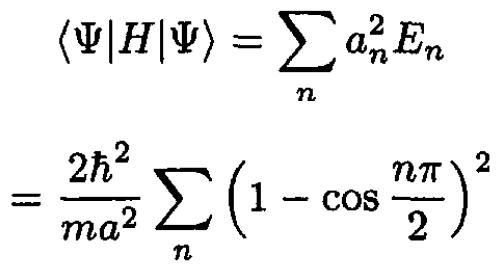 (5)
(5)
This latter series does not converge. It takes an infinite amount of energy to form the initial wave function.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


