
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Spin–Orbit Interaction
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 68
22-8-2016
2095
Spin–Orbit Interaction
Consider in three dimensions an electron in a harmonic oscillator potential which is perturbed by the spin–orbit interaction
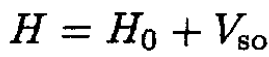 (i)
(i)
 (ii)
(ii)
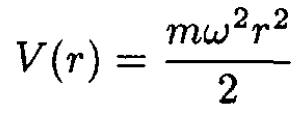 (iii)
(iii)
 (iiii)
(iiii)
a) What are the eigenvalues of the ground state and the lowest excited states of the three-dimensional harmonic oscillator?
b) Use perturbation theory to estimate how these eigenvalues are altered by the spin–orbit interaction.
SOLUTION
a) In three dimensions the lowest eigenvalue of the harmonic oscillator is (3/2)hω, which can be viewed as hω/2 from each of the three dimensions. The ground state has s-wave symmetry. The lowest excited states have eigenvalue (5/2)hω. There are three of them. They have p-wave symmetry and are the states L = 1 and ML = (1,0, -1).
b) In the spin–orbit interaction we take the derivative ∂V/∂r and find
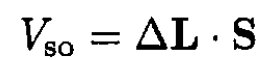 (1)
(1)
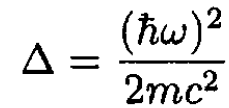 (2)
(2)
The matrix element ∆ is a constant, which simplifies the calculation. We evaluate the factor L . S by defining the total angular momentum J as
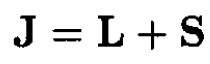 (3)
(3)
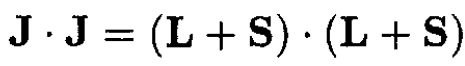 (4)
(4)
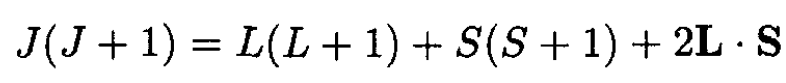 (5)
(5)
 (6)
(6)
For the ground state of the harmonic oscillator, L = 0 and J = S = 1/2. The above expectation value of L . S is zero. The ground state is unaffected by the spin–orbit interaction, although it is affected by relativistic corrections as well as by other states.
The first excited states have L = 1, S = 1/2 so that J = 3/2, 1/2. For J = 3/2 we find that
 (7)
(7)
For J = 1/2 we find that
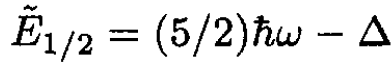 (8)
(8)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















