
Iterated Capacitance
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 52
الجزء والصفحة:
part 1 , p 52
 9-8-2016
9-8-2016
 1774
1774
Iterated Capacitance
a) Given two point charges of opposite sign and unequal in magnitude, show that the (nontrivial!) surface V = V (∞) with is a sphere. Find its radius and center. This is the basis of the “method of images” for problems involving equipotential spheres.
b) Describe concisely but clearly an iterative method to find the capacitance of two conducting spheres of radius a whose centers are 4a apart.
c) Calculate the capacitance to within 5%.
SOLUTION
a) We found in Problem 3.5 that a charge a distance R from a conducting sphere of radius a produced an image charge q' a distance r from the center of the sphere, where
 (1)
(1)
Using this result, we may verify that charges q and q' a distance R – r

Figure 1.1a
apart do indeed give a spherical equipotential surface. The problem is cylindrically symmetric, so we establish a circular equipotential by writing down the potential due to the two charges (see Figure 1.1a). Given that V(∞) = 0, we find the sum of the potentials
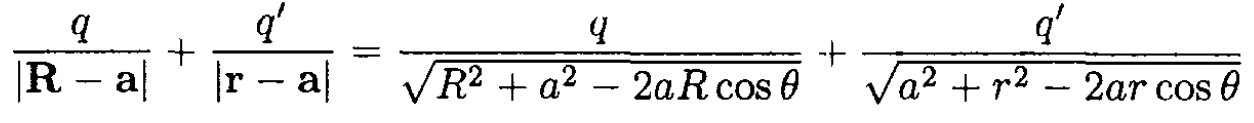
for a circle of radius a. If q' = -qa/R, we have

With r = a2/R,

as required. Given that the separation of the two charges is some distance x = R – r, we may find the radius of the sphere a and the location of the center with respect to one of the charges R using (1):

b),c) In general, the charge and potentials of a number of conductors are related by the linear equations
 (2)
(2)
where Cii and Cij are called coefficients of capacity and induction, respectively.
In the case of two conductors carrying equal but opposite charges, the capacitance is defined by the ratio of the charge on one conductor to the potential difference between them. For our two-sphere capacitor, we have
 (3)
(3)

Figure 1.1b
The capacitance may be found by setting q2 = -q1 and calculating
 (4)
(4)
If we choose the zero of potential at infinity, it is clear that V2 = – V1 so we have for the capacitance
 (5)
(5)
This is a specific case of a more general result
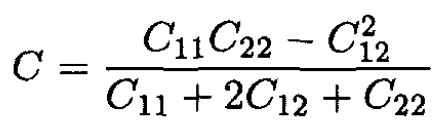 (6)
(6)
Now we may calculate C11 and C12 by placing a charge Q on the first sphere, giving it a potential V = Q/a, then placing an image charge inside the other sphere to keep it at zero potential. In turn, we place an image charge inside the first sphere to restore the potential to Q/a, whereupon we. ... Operationally, we have from (1) (see Figure 1.1b)

c) For our problem, R = 4a, and Q0 = Q, so we find Q1 = -Q/4, Q2 = Q/15, Q3 = -Q/56, and Q4 ≈ Q/209. Since we maintain V2 = 0, we have from the first of (3)
 (7)
(7)
So
 (8)
(8)
Since C12 = C21, we find from the second of (3) by summing the first two image charges in sphere 2
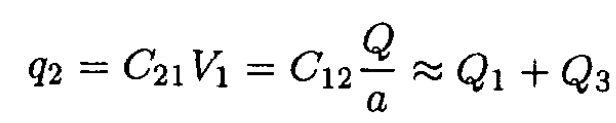 (9)
(9)
So
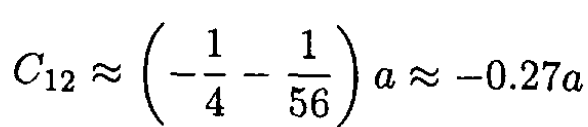 (10)
(10)
Finally, we have
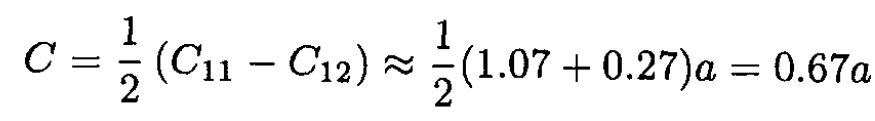 (11)
(11)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


