Vibrating String with Mass

A thin uniform string of length L and linear density ρ is stretched between two firm supports. The tension in the string is T (see Figure 1.1).

 Figure 1.1

a) Derive from first principles the wave equation for small transverse disturbances in the string.

b) Determine the set of possible solutions for the given boundary conditions and state the allowed frequencies.

c) A small mass m is placed a distance l from one end of the string. Determine the first-order correction to the frequencies of the modes found in (b).

SOLUTION

a) To derive the equation of motion of the string we assume that the oscillations of the string are small, the tension T is a slowly varying function

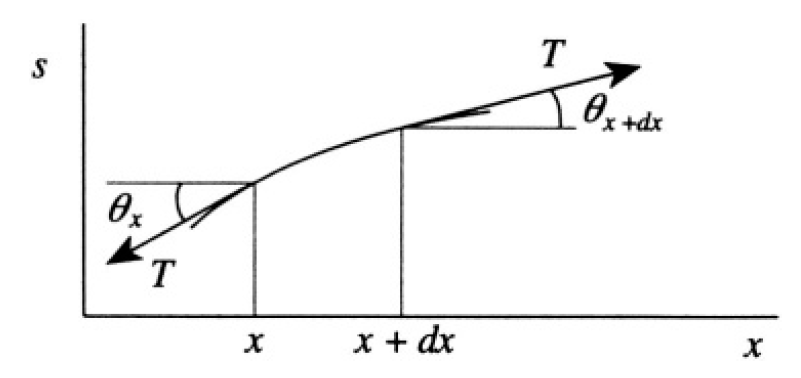
Figure 1.2

of x, and there is no damping of the motion. Consider a part of the string between x and x + dx, where s (x, t) is the transverse displacement of the string (see Figure 1.2). The transverse force acting on this piece of mass ρdx is

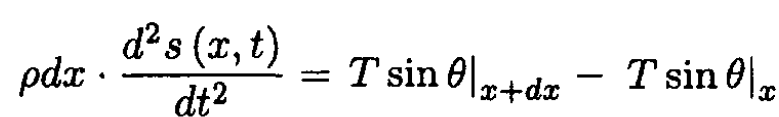(1)

Using the initial assumptions, we can substitute a constant T for the tension T(x) and write

(2)

where the substitution of tan θ for sin θ again follows from assumptions. Using (2) in (1), we obtain

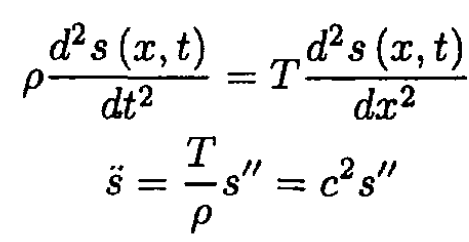(3)

where is the wave velocity.

b) Now, we have boundary conditions. We choose a standing wave solution. Another possible solution is a traveling wave s (x, t) = f(x + ct) + g (x – ct), where f and g are some functions. In our case, we use the method of separation of variables: s (x, t) = g(x) f(t), which, substituted into (3), gives

where ω² is a constant independent of x and t. We arrive at two secondorder differential equations for f and g and their solutions:

Applying the boundary condition to the solution:

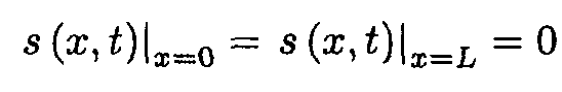
from which we get

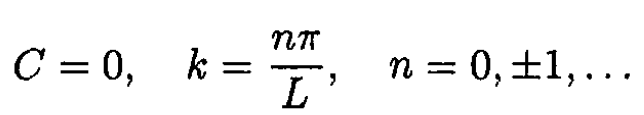
For each mode g_n (x) = sin (ω_n x/c) and f_n (t) = A_n cos ω_nt + B_n sin ω_nt with ω_n ≡ ncπ/L. For each complete mode

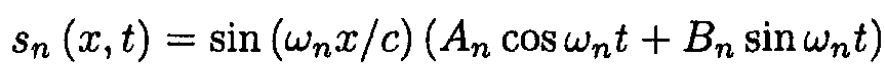
and the transverse displacement is

c) To find the frequency change, use a perturbation method. Consider for simplicity the nth mode of the form s_n = sin(nπx/L) cos ω_nt,  corresponding to the initial conditions s (x, 0) = s₀ (x) and  We know from the virial theorem that initially the average of potential energy of the string in the nth mode is equal to the kinetic energy:

(4)

where we used  Now examine the mode of the string with mass to be of the same form as in (S.1.46.4): s_n (x, t) = sin(nπx/L) cos Ω_nt  with a slightly different frequency Ω_n. Find the kinetic energy  in this mode of the string and then add the kinetic energy of the additional mass:

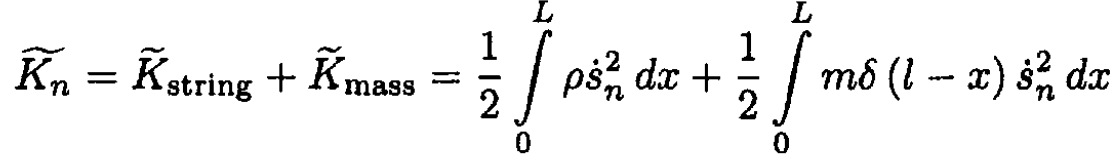
where δ (l – x) is the Dirac δ function. The average kinetic energy of the string with mass from (5)

(6)

where again we used 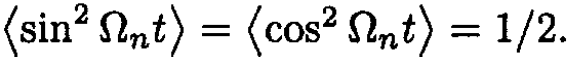 In this approximation, if we ignore the change in tension T, the average potential energy of the string with mass is the same as for the string alone, so  Utilizing this together with the virial theorem, which is also true for the modified string, we may write

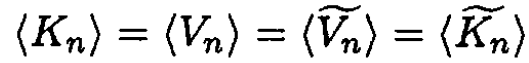(7)

So from (5)–( 7)

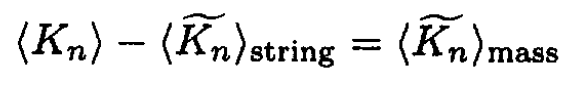
or

(8)

Therefore the new frequency

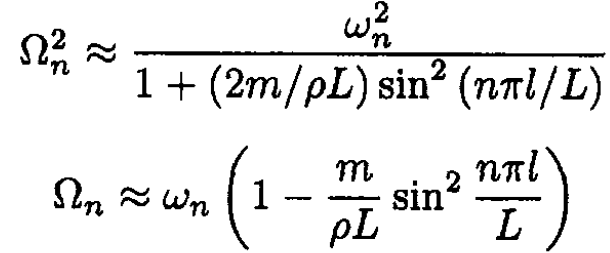(9)

where we used m << ρL.