
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تحويلات لورانتز Lorentz transformations
المؤلف:
محمد فخري
المصدر:
النظرية النسبية
الجزء والصفحة:
.....
24-7-2016
11089
تحويلات لورانتز Lorentz transformations
نفرض إطاران مرجعيان ساكنان S, S/ و النظام S/ يتحرك بسرعة منتظمة v في الاتجاه الموجب لمحور X كما هو موضح من الرسم (انظر تحويلات جاليليو).فإذا وقع حدث معين (وميض مثلا) عند النقطة A و أن هناك مراقبين رصدا هذا الحدث بحيث أن t = t/ = 0 عندما كانت o/ منطبقة على o أي عندما x = x/ = 0. اذا اصدر المراقب الموجود في S/ وميضا فانه بعد زمن t/ يجد نفسه هذا المراقب في مركز كرة ضوئية نصف قطرها r/ = ct/ حيث c سرعة الضوء. و معادلة هذه الكرة على الصورة
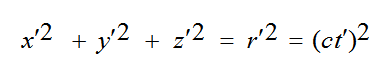 (1)
(1)
و بالمثل يجد نفسه المراقب S بعد زمن t في مركز كرة ضوئية معادلتها هي :
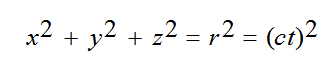 (2)
(2)
نلاحظ من المعادلتين السابقتين أن سرعة الضوء واحدة لم تتغير بالنسبة للمراقبين أو بالنسبة للإطارين، و هذا يتفق مع الفرض الثاني للنظرية النسبية الخاصة. و نلاحظ أيضا أن معادلة الدائرة لها نفس الصيغة الرياضية في الحالتين و هذا يتوافق مع الفرض الأول لأينشتين.
التحويلات المطلوبة هي عبارة عن المعادلات التي تربط بين المتغيرات(x, y, z, t) و المتغيرات (x/ , y/, z/, t/) و التي يمكن من خلالها تحويل أي من المعادلتين إلى المعادلة الأخرى.
و بدراستنا للإطارين المرجعيين S, S/ نلاحظ أن الاختلاف بين المعادلتين السابقتين يرجع فقط الى المتغيرات (x, t) و (x/, t/). و بذلك فان معادلات التحويل y = y/ و z = z/ لا ينتج عنها أي اختلاف ( حيث أن الفضاء متماثل). و بسبب تماثل الفضاء و انتظام قوانين الطبيعة فيمكن افتراض أن معادلات التحويل بين المتغيرات (x , t) و (x/ , t/) هي معادلات خطية يمكن أن تكتب على الصورة:
 (3)
(3)
 (4)
(4)
حيث أن a1, a2 , b1 b2 هي ثوابت يجب تعينها لمعرفة معادلات التحويل.
و عندما يكون x/ = 0 أي في مركز الإسناد S/ يكون x = v t و بالتعويض بهذه القيمة في المعادلة (3) نحصل على:
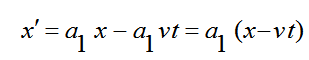 (5)
(5)
و بالتعويض من المعادلتين (4) و (5) في المعادلة (1) مع الأخذ في الاعتبار أن y = y/ و z = z/ يمكننا الحصول على:

و هذه المعادلة تأخذ الصورة الأتية:
 (6)
(6)
و بمقارنة معاملات المعادلتين (6) و (2) نحصل على:
 (7)
(7)
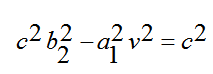 (8)
(8)
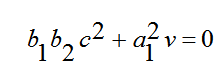 (9)
(9)
و بحل المعادلات الثلاثة الأخيرة يمكننا الحصول على:
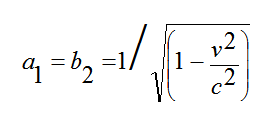 (10)
(10)
 (11)
(11)
و بالتعويض من المعادلة (20) في المعادلة (15) نحصل على العلاقة الاتية:
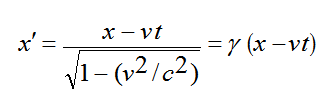 (12)
(12)
حيث أن
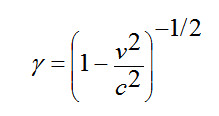
و يسمى γ معامل لورنتز.
و بالتعويض من المعادلتين (20)و (21) في المعادلة (14) نحصل على العلاقة:
 (13)
(13)
و بذلك تصبح معادلات التحويل هي:
 (14)
(14)
تعرف هذه المعادلات الأربعة بتحويل لورنتز نسبة للعالم الهولندي Lorentz و الذى حصل عليها عام 1903 أي قبل النظرية النسبية لأينشتين بعامين. هذا و قد حصل لورنتز على هذه المعادلات أثناء دراسة حركة الجسيمات المادية في المجال الكهرومغناطيسي. و لكن لم يفطن لورنتز إلى أهمية هذه المعادلات، حيث استخدم السرعة v لكى تعبر عن سرعة الجسيم بالنسبة للأثير ( و الذى لا وجود له في الحقيقة). و عندما جاءت النظرية النسبية لأينشتين و استخدمت هذه المعادلات بمعالجة مختلفة، حيث تشير v في هذه الحالة أن النظام S/ يتحرك بسرعة منتظمة v بالنسبة للنظام S .
و لذلك تسمى هذه المعادلات أحيانا معادلات لورنتز – أينشتين و التي تعتبر الأساس للنظرية النسبية لأينشتين.
و يمكننا الحصول تحويل لورنتز – أينشتين العكسي إذا افترضنا أن إطار الإسناد S/ يتحرك بسرعة v- بالنسبة لإطار الإسناد S. و يمكننا ذلك رياضا بالتعويض عن v ب v- و نستبدل القيم ذات الشرطة بنظيراتها بدون شرطة كما يلى
 (15)
(15)
 الاكثر قراءة في النظرية النسبية الخاصة
الاكثر قراءة في النظرية النسبية الخاصة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















