إذا كان نظام ما مكوَّنًا من جسيمات مرقمة عدديًا بالدليل i، وتقع عند مواضع 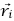، فإن موضع مركز الكتلة  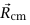يعرف بالمعادلة:

بالكلمات، متجه الموضع لمركز الكتلة هو المتوسط الموزون لمتجهات موضع الجسيمات المفردة، وكل جسيم يوزن بنسبة كتلته إلى الكتلة الكلية. إذا كانت X_cm, Y_cm, Z_cm هي الإحداثيات الكارتيزية لمركز الكتلة، فإن المعادلة (16–4) تكون مكافئة للمعادلات الثلاث:

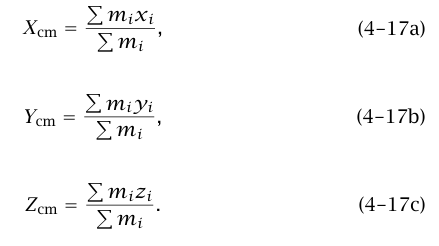
إذا أعدنا كتابة المعادلة (16–4) على الصورة 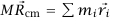؛ حيث M = ∑m_i، وأجرينا عملية التفاضل لكلا الجانبين بالنسبة إلى الزمن، نحصل على:

حيث . بتفاضل كلا الجانبين بالنسبة إلى الزمن مرة ثانية، نحصل

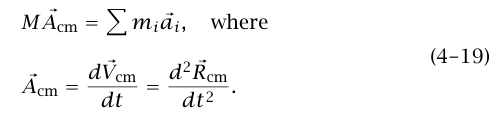
بضم هذه النتيجة إلى المعادلة (10–3) نحصل على النتيجة المهمة جدًّا التالية:

التي تنص على أن حركة مركز كتلة نظام ما تماثل حركة جسيم كتلته (حيث M الكتلة الكلية للنظام يتعرض لقوة 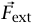 (حيث 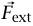 القوة الخارجية الكلية المؤثّرة هي على النظام)؛ ولهذا، إذا ألقيت كرسيا في الهواء بأي قدر من اللف، فإن مركز الكتلة (يختصر بوجه عام إلى (CM للكرسي سوف يتحرّك (نهمل هنا احتكاك الهواء) في شكل قطع زائد.

القوة الخارجية في مثال 4–4 تساوي صفرًا؛ ومن ثُمَّ 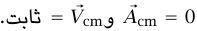 وبما أنه في البداية 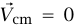، فإنه ينتج أن  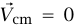دائما، و 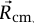قيمة ثابتة. وعلى ذلك فإن مركز الكتلة لا يتحرك أبدًا، ويجب أن يحدث التصادم عند مركز كتلة الموضعين الابتدائيين.

كثيرًا ما يهتم امرؤ ما بحركة جسم جاسئ محدود الحجم (أي ليس متناهيا في الصغر). وغالبًا ما يكون موضع مركز الكتلة واضحًا من اعتبارات التماثل (على سبيل المثال، مركز كتلة قضيب منتظم يقع عند النقطة الوسطى). لكن في حالات أخرى يكون بعض الحساب ضروريًا نموذجيًا، نجزّئ مفاهيميًّا عمليات الجمع في المعادلات (a17–4) و(b17–4) و(c17–4) بواسطة حساب التكامل كمثال، دعنا نحسب موضع مركز الكتلة CM لنصف كرة جاسئة كثافتها منتظمة للتبسيط. نأخذ المحورين x وy في الوجه المسطح، ونقطة الأصل عند مركز ذلك الوجه. نرى من اعتبارات التماثل البسيطة أن مركز الكتلة يقع على المحور z؛ أي إن 0 = X_cm = Y_cm. لحساب Z_cm، علينا أن نحوّل المجموع في المعادلة (c17–4) إلى تكاملات، ويمكن عمل ذلك ببساطة بإحدى طريقتين؛ في الطريقة الأولى نقسم الجسم إلى شرائح رقيقة بواسطة مستويات عمودية على المحور z مستوى z الثابت يقطع نصف الكرة في دائرة نصف قطرها ؛ حيث a نصف قطر نصف الكرة؛ بهذا نجد أن حجم الشريحة المحتواة بين المستوى على ارتفاع z والمستوى على ارتفاع z + dz هو dz(²z – a²)π، وكتلة هذه الشريحة هي dz(²z – a²)ρπ؛ حيث كثافة الكتلة (كتلة وحدة الحجم). بتحويل الجموع في المعادلة (c17–4) إلى تكاملات، نجد أن:

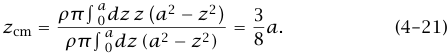
بدلا من ذلك نستطيع أن نقسم الجسم إلى عناصر حجم معرفة بأسطح الإحداثيات الطبيعية في إحداثيات كروية الحجم. وحجم العنصر هو dV = r² sin θ dr dθ dФ. باستخدام
z = r cos θ ، نجد أن:

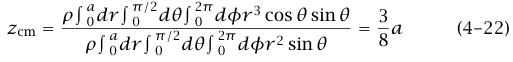
بما يتفق مع الحساب السابق. لاحظ أن الإجابة معقولة؛ ونتوقع أن يكون 2/z_cm < a؛ حيث إن أكثر من نصف الكتلة موجود تحت المستوى 2/z = a.

ملحوظة. يمكنك ، إذا كنت مهتمًا، أن تحسب موضع مركز الكتلة لأجسام متنوعة، لهرم على سبيل المثال. هذا تمرين في حساب التفاضل والتكامل أكثر منه في الفيزياء.

إذا تحرك نصف الكرة الجاسئة إلى موضع مختلف، أو أُميل، فإن مركز الكتلة يستمر ليكون نفس النقطة الفيزيائية للجسم. وبصورة أعم، تعريف مركز الكتلة (المعادلة (16–4)) يعني ضمنًا أن مركز كتلة جسم جاسئ يستمر في أن يكون نفس النقطة الفيزيائية للجسم حتى عندما يتغير موضع الجسم واتجاهه. وبالنسبة إلى بعض الأجسام، مثل كرة مفرغة، لا يهم وضعها عند مركز الكتلة. وبرغم ذلك، يستطيع المرء أن يتخيَّل مركز الكتلة متصلا بالجسم عن طريق قضبان لا وزن لها.

افترض أننا قسمنا الجسيمات في نظام ما إلى مجموعتين (نظامين فرعيين) نسميهما 1 و2. افترض أن الكتلتين الكليتين للنظامين الفرعيين هما ₁M وM₂، وأن مركزي كتلتيهما يقعان عند 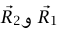. عندئذ ينتج من تعريف مركز الكتلة، المعادلة (16–4)، أن مركز كتلة النظام ككل ما هو إلا مركز كتلة الكتلتين النقطيتين. تقع M₁ عند 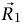وM₂ عند 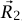؛ وبناءً على ذلك، إذا التحم قضيبان معًا، فإن مركز كتلة النظام المركب منهما يكون تماما مركز كتلة الكتلتين النقطيتين اللتين تقعان عند نقطتي منتصف القضيبين.

المعادلة (20–4) ذات فائدة عملية مهمة عندما تُطبَّق على جزء من نظام دوار مثل الحدافة. إذا كانت الحدافة تدور حول محور ثابت، فإن أي نقطة فيزيائية عليها تتحرك في دائرة. افترض أن مركز كتلة الحدافة لا يقع على المحور؛ عندئذٍ يتحرك مركز الكتلة في دائرة، وتكون له عجلة مقدارها v²/R وتتجه نحو المركز؛ حيث v مقدار سرعة مركز الكتلة وR بعد مركز الكتلة عن المركز. إذا كانت الحدافة تدور n دورة في الثانية (يُطلق على n التردد) فإن v = 2πRn وv²/R = 4π²n²R. إذا كانت كتلة الحدافة M، فإن المعادلة (20–4) تنص على أن قوة خارجية مقدارها 4π²n²RM يجب تطبيقها على الحدافة. هذه القوة يبذلها محور التحميل وتتجه قطريا إلى الداخل، بطول الاتجاه اللحظي من مركز الكتلة إلى المحور تؤثّر الحدافة على محور التحميل بقوة مساوية في المقدار ومضادة في الاتجاه، ترهق أجزاء التحميل أو تجعلها تتذبذب، أو تسبب الأثرين معًا. على سبيل المثال، إذا كانت كتلة الحافة 145kg  وتدور 6000 دورة كل دقيقة (100 n =)، وإذا كان مركز الكتلة يبعد 3.175 مليمترات (1/8 بوصة) عن المحور، فإن مقدار هذه القوة الدوارة بسرعة هو 182000 نيوتن، أو 40800 رطل، أو أكثر من 20 طنا. لكي تكون 0 = R توصل كتلة نقطية بالحدافة، بحيث يؤدي اختيار مقدار الكتلة النقطية وموضعها إلى وضع مركز الكتلة على المحور. يُسمى هذا الإجراء الموازنة الاستاتيكية للحدافة.

إضافة لمالكي السيارات

حتى بعد موازنة جسم ما استاتيكيًّا، فإنه قد يظل مؤثرًا بقوة على أعمدة التحميل. اعتبر، على سبيل المثال، النظام (شكل 4–2) المكون من محور AB والدمبل الملحوم به. اللحام عند مركز كتلة الدَّمبل، لكن الزاوية θ بين الدَّمبل والمحور لا تساوي °90. يدور الدمبل والمحور حول الاتجاه AB، والمحور يرتكز على عمودي تحميل عند A وB. بما أن مركز الكتلة يقع على المحور فإنه لا يتسارع؛ ومن ثَمَّ لا يبذل عمود التحميل أي صافي قوة (إلا في حالة قوة ثابتة إلى أعلى تساوي وزن الدمبل والمحور). ومع ذلك فإنه في أي لحظة يؤثّر عمود التحميل عند A وB بقوتين على المحور متأرجحتين، متساويتين في المقدار ومتضادتين في الاتجاه، فإنه يتلاشى «ميل» الدمبل لأنه يصطف عموديا على محور الدوران. تتلاشى هاتان القوتان المتأرجحتان بتأثير موازنة ديناميكية.

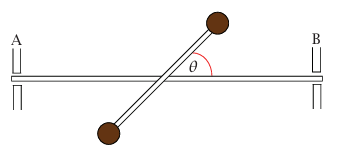
شكل 4–2: دمبل على محور.